Om de werking van de hersenen beter te begrijpen, willen neurowetenschappers tot in detail weten welke hersengebieden met elkaar in verbinding staan. Diffusie-MRI maakt dat in principe zichtbaar, maar er moet nog veel aan verbeterd worden. Dankzij subtielere wiskunde zijn nu ook kruisende zenuwbanen te onderscheiden.
Diffusie-MRI-scans leveren iconische beelden op. De hersenen vertonen zich als een glossy: veelkleurige kluwen zenuwbundels die door een dure coiffeur in model gebracht zijn. Volgens Tom Dela Haije, onlangs aan de TU Eindhoven gepromoveerd op dit onderwerp, klopt die indruk: “In zo’n plaatje zit uren werk van iemand die precies weet hoe die zenuwbanen behoren te lopen, en die de valspositieven eruit haalt. Automatische methodes om dat te doen zijn niet betrouwbaar.”
Valspositieven zijn, in dit geval, verbindingen tussen hersengebieden die opduiken in de scans, terwijl ze er niet echt zijn. Een MRI-scan is nooit een eenduidige afbeelding van de werkelijkheid zoals een onbewerkte foto, het is altijd een product van intensieve computerberekeningen op een grote, abstracte dataset.
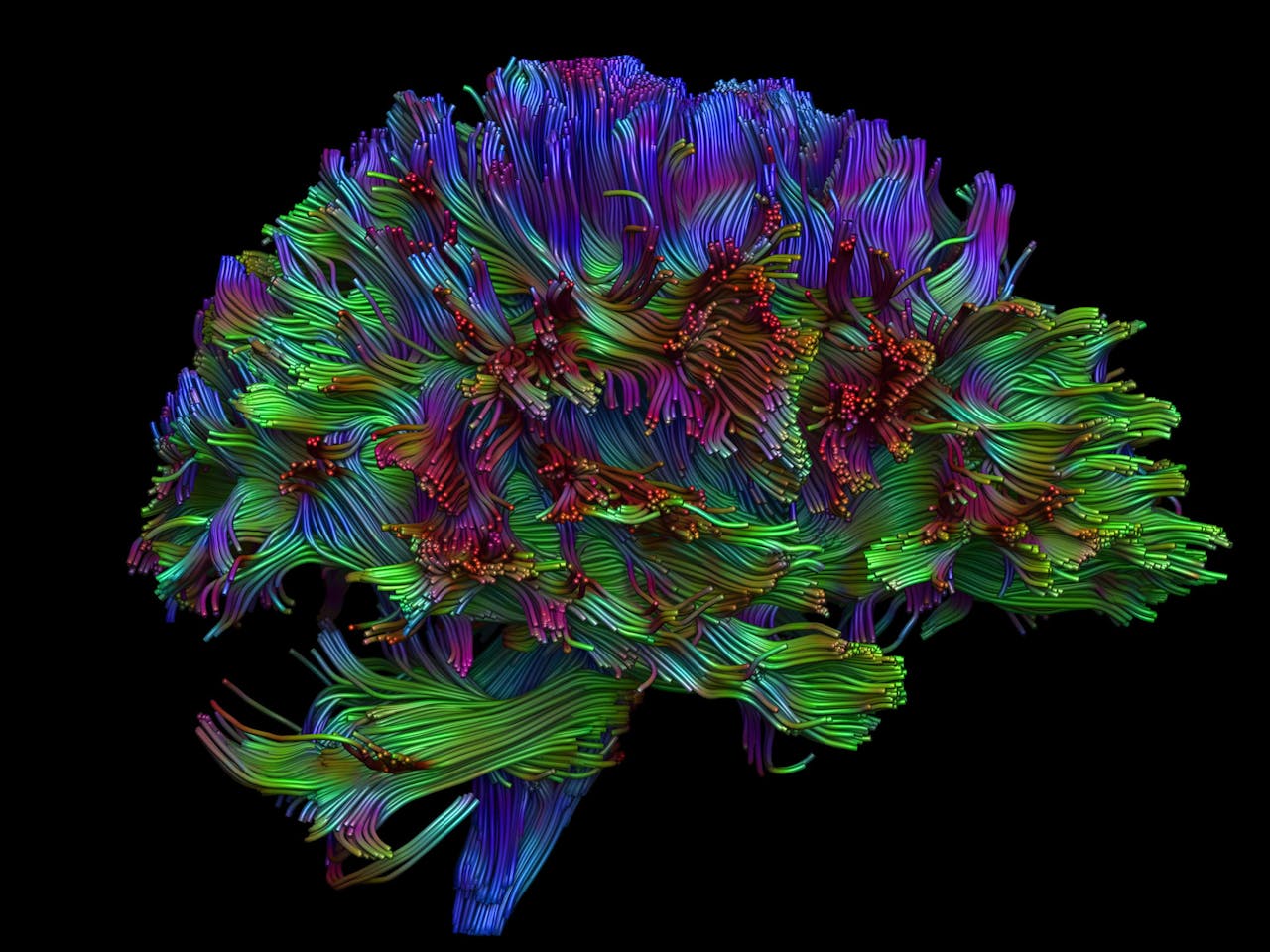
Conventioneel diffusie-MRI-beeld van de hersenen. Tom Dela Haije: “In zo’n plaatje zit vaak uren handwerk van iemand die precies weet hoe die zenuwbanen behoren te lopen.”
Alexander LeemansDiffusie
Diffusie-MRI gaat nog een stap verder: de radiostraling die de watermoleculen uitzenden, vertelt ook welke snelheid ze hebben. Moleculen in een vloeistof bewegen altijd chaotisch door elkaar heen – diffusie – maar als het water in een microscopisch nauw buisje zit, heeft die chaotische beweging een voorkeursrichting: er is meer diffusie in de lengte dan in de breedte van het buisje, en dit is af te lezen aan het radiosignaal dat de gemagnetiseerde moleculen uitzenden. Een vergelijkbaar principe is van toepassing in het brein. Omdat zenuwcellen via lange, dunne uitlopers – axonen – contact met elkaar leggen, kan diffusie-MRI in beginsel verbindingen in het brein opsporen.
Maar de praktijk is verre van simpel. Dela Haije: “Watermoleculen hebben interactie met alles, en hersenweefsel is heel complex.” En de dataset die één scan oplevert is enorm. Een voxel (een pixel in een 3D-beeld) van een moderne MRI-scan is, in de hoogste resolutie, ongeveer 1 × 1 × 1 millimeter, dus een scan van een heel brein (ongeveer anderhalve liter) omvat 1,5 miljoen voxels. Iedere voxel moet tientallen keren worden bekeken om een indruk te krijgen van de moleculaire bewegingen, en bij elke meting hoort een complex radiosignaal dat het gemiddelde is van miljoenen watermoleculen.
Voxels
Deze enorme dataset, met heel veel ruis erin, moet drastisch gereduceerd worden om er nuttige informatie – een ‘plaatje’ – uit te halen. Een veel gebruikte manier om dit te doen is om de data van alle voxels weer te geven als punten in een zogeheten Riemannse geometrie. Dit is een abstracte ruimte met zes dimensies: drie ruimtedimensies en drie dimensies die overeenkomen met de x-,y- en z-component van de diffusiesnelheid in elke voxel.
Als je een scan zou maken van een schedel vol stilstaand water, lijkt de Riemannse geometrie sterk op de gewone, rechttoe rechtaan ruimte zoals wij die kennen, afgezien van het dubbele aantal dimensies. Maar als je water in hersenweefsel scant, verschilt de diffusiesnelheid per richting en per voxel. Dit komt overeen met een ruimte die vervormd is: die kan lokaal gekrompen, uitgerekt of verwrongen zijn. De verwringing van deze ruimte bepaalt uiteindelijk welk hersenverbindingen het plaatje van de diffusie-MRI-scan laat zien.
Echter, de Riemannse geometrie kan slechts op een paar simpele manieren vervormd worden. Het wiskundige gereedschap dat de computer gebruikt om de ruwe dataset te verwerken tot een plaatje is daar op afgestemd. Een van de nadelen is dat de Riemannse geometrie alleen informatief is wanneer de zenuwbanen in een voxel slechts in één richting lopen. Lopen er evenveel zenuwbanen verticaal als horizontaal door die voxel, dan zijn deze zenuwbanen in deze geometrie effectief onzichtbaar.
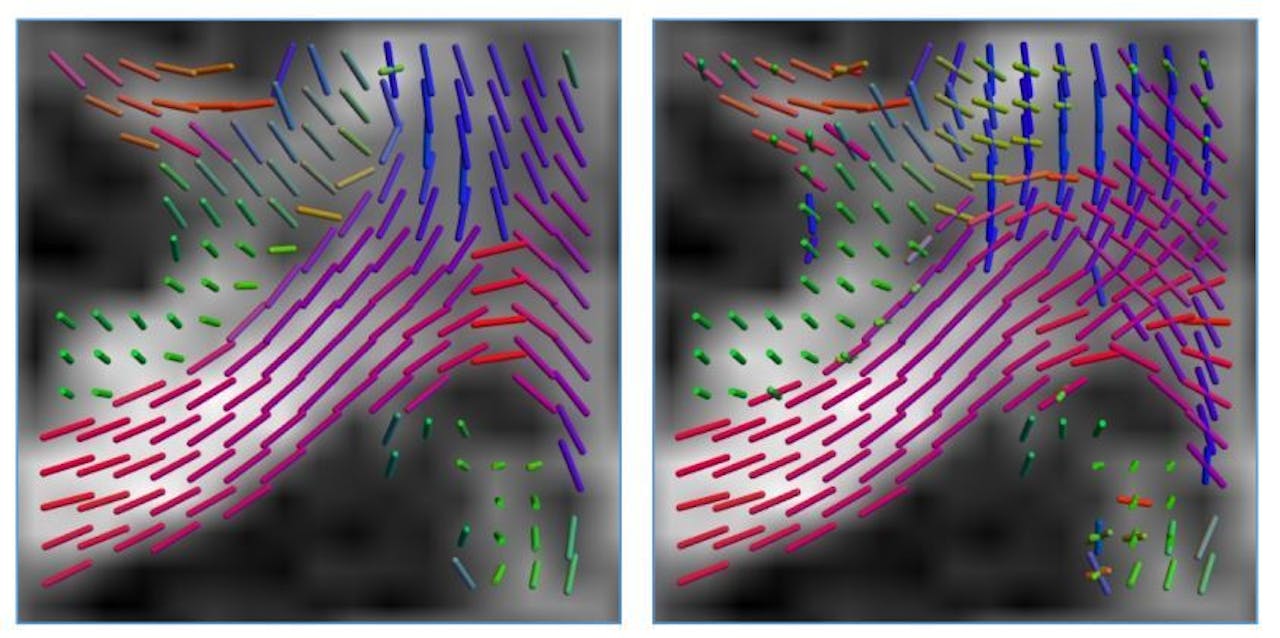
Als zenuwbanen elkaar kruisen, is dat in de nu gebruikelijke manier van data analyseren niet te zien (links). Door het gebruik van de Finsler geometrie, wordt dit wel zichtbaar (rechts).
Tom Dela HaijeIngewikkeldere vervormingen
Dela Haije onderzocht in zijn proefschrift onder meer of de Finsler geometrie hier soelaas kan bieden. De Finsler geometrie laat ingewikkeldere vervormingen van de ruimte toe. Daardoor is het wel mogelijk om elkaar kruisende zenuwbanen weer te geven (zie rechter afbeelding voor een schematisch voorbeeld).
Uit zijn onderzoek bleek dat de Finsler geometrie in simpele patronen van zenuwbanen net zo goed presteert als de Riemannse geometrie, en in gecompliceerde situaties beter. Tot nu toe heeft hij dit uitgeprobeerd op openbare diffusie-MRI-datasets van gezonde proefpersonen.
Hoewel deze geometrische methodes voor een leek moeilijk te begrijpen zijn, en misschien overdreven abstract lijken, vormen ze een machtige gereedschapskist. Dela Haije: “Door deze aanpak kunnen we de resultaten van honderden jaren wiskundig onderzoek gebruiken.”
Dela Haije werkt inmiddels in Denemarken verder aan nog geavanceerder technieken voor de analyse van diffusie-MRI-scans: “Hoe veel informatie kunnen we er nog méér uithalen? Dat willen we beter begrijpen.”
Valspositieven
Dat blijft hard nodig, want diffusie-MRi is nog lang niet perfect. In een groot overzichtsartikel dat vorig jaar op BioRXiv (een online archief met natuurwetenschappelijke artikelen) verscheen, wordt zelfs gesteld dat de meeste zenuwbanen die uit diffusie-MRI-scans opduiken, valspositieven zijn. Dela Haije: “Sommige grote zenuwbanen kunnen we met zulke scans redelijk goed inschatten, bijvoorbeeld tussen de ogen en de visuele cortex, die in het achterhoofd ligt. Dat kan bruikbaar zijn, want die wil je bij operaties graag ontwijken. Maar over het gehele brein bekeken, zijn zenuwbanen nu nog niet automatisch te reconstrueren.”
Maar in menig opzicht is diffusie-MRI het beste wat we hebben om de organisatie van het brein te doorgronden: “Het grote voordeel van diffusie-MRI is dat je levend weefsel kunt bekijken; dood hersenweefsel verliest binnen een paar uur al veel structuur. Als alternatief kun je nog proberen om hersens snel in te vriezen, in heel dunne plakjes te snijden en met de microscoop de verbindingen te volgen. Maar het gaat om miljarden zenuwbanen die elk maar een duizendste millimeter dik zijn. Het is een enorme uitdaging om al die plakjes exact op elkaar te laten passen. Uiteindelijk moeten deze methodes allemaal samen worden gebruikt, om de een met de ander te valideren.”