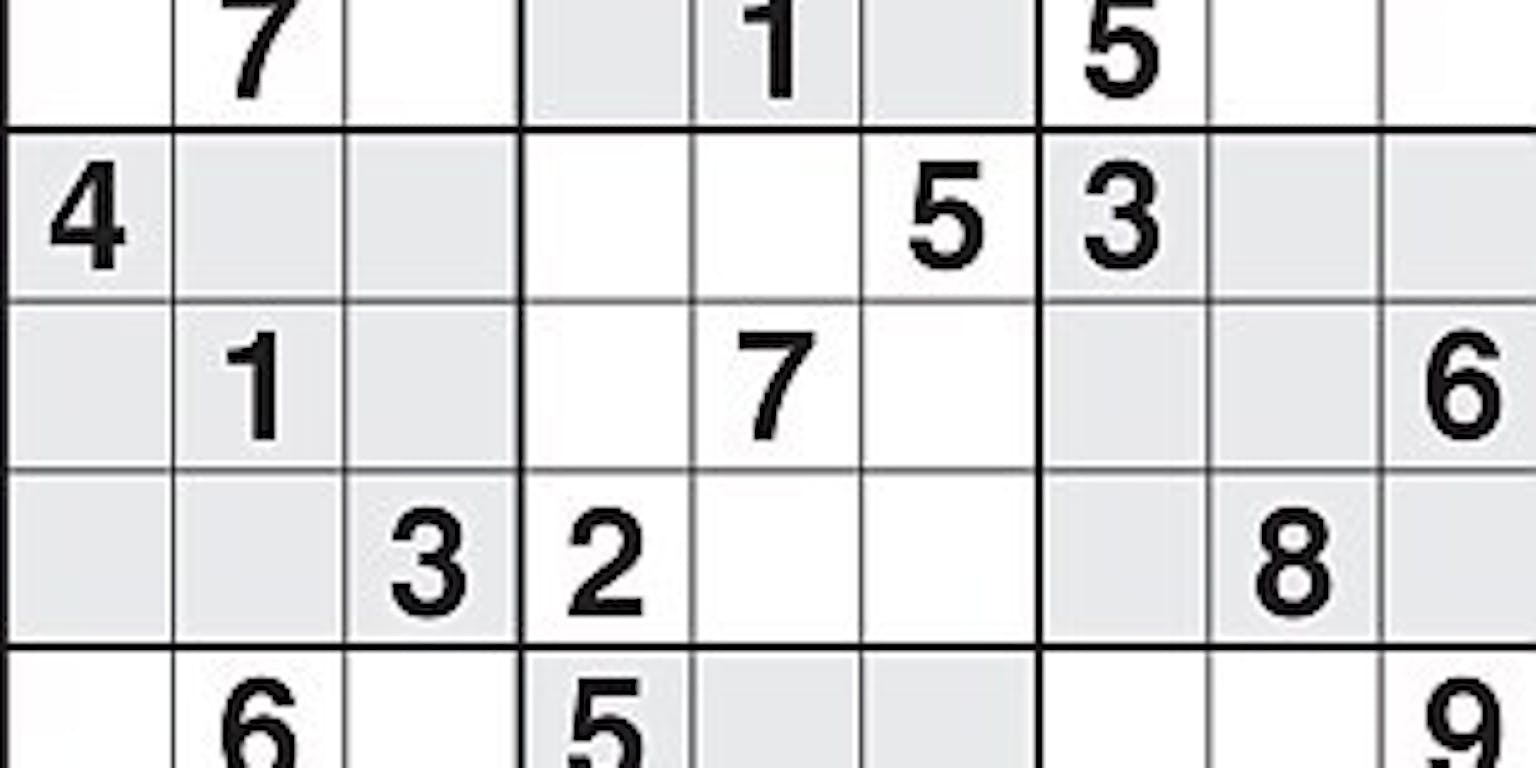
Sudoku’s zijn leuke puzzels, maar soms kom je er niet uit. Dan is het handig om ze met behulp van een computer op te kunnen lossen. Wiskundigen aan de Amerikaanse universiteit van Notre Dame hebben een nieuwe manier bedacht om sudoku’s op te lossen.
Sudoku’s zijn soms best lastig. Zou het niet mooi zijn als er een computerprogramma bestond om een sudoku op te lossen? Goed, het neemt het hele plezier van de puzzel weg, maar je hebt in ieder geval de oplossing.
Dat soort programma’s bestaat al, maar deze gebruiken vaak een bepaalde manier om de getallen te bepalen. Ze doen dit door middel van ‘_backtracking_’. Daarbij gok je als het ware welk getal er op een plek kan staan en vervolgens werk je de sudoku verder uit. Als dan blijkt dat je gok problemen oplevert, ga je terug naar het begin, met een nieuw getal.
Omdat computers dit soort berekeningen veel sneller kunnen maken dan mensen, lijkt het alsof je soduka heel snel goed wordt ingevuld, maar op de achtergrond gaat het mis totdat het goede antwoord is gevonden. Dat kost veel tijd en erger nog, als de sudoku te ingewikkeld wordt komen er veel fouten. Probeer maar eens de sudoku hieronder op te lossen met het programma.
Voorspelbaar algoritme
Hoe los je zo’n ingewikkelde sudoku dan op, als het niet met de hand lukt? Wiskundigen van de Amerikaanse universiteit van Notre Dame, Zoltan Toroczkai en Maria Ercsey-Ravasz, hebben nu een nieuw algoritme gebruikt, dat géén gebruikt maakt van backtracking. Hun algoritme is deterministisch, oftewel voorspelbaar. Een deterministisch algoritme kan je zien als een wiskundige functie. Het geeft voor elke waarde die je kan invullen een voorspelbaar en eenduidig antwoord. Dit in tegenstelling tot de backtracking-methode, die gebruik maakt van willekeur om een getal in de sudoku in te vullen.
Het voordeel van de deterministische methode: je bent korter bezig en je kan met zekerheid moeilijkere sudoku’s oplossen. Het oplossen van een moeilijke puzzel duurt alsnog tien keer zo lang als het oplossen van een makkelijke puzzel, maar de oplossing klopt wel. Hoe het algoritme precies werk is erg ingewikkeld. Allereerst verdeel je de sudoku in negen lagen; een laag voor elk getal dat kan voorkomen in de sudoku. Vervolgens vul je elke laag in met enen en nullen.
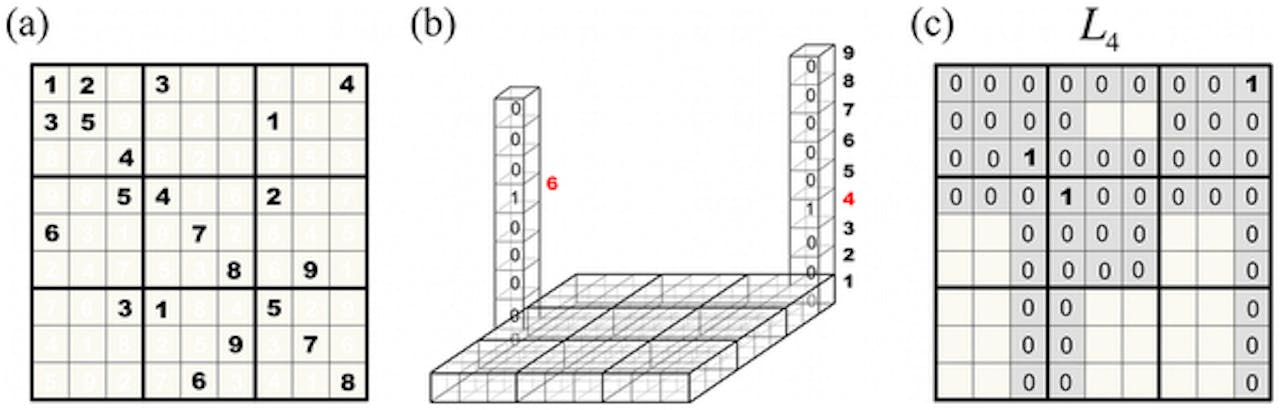
Voorstelling van het algoritme. Het middelste plaatje laat een deel van de kubus zien, die ontstaat na het onderverdelen van een sudoku in negen lagen.
Zoltan Toroczkai en Maria Ercsey-RavaszOp alle plekken waar de hints (de getallen in een sudoku die van te voren ingevuld zijn) staan, komt een 1 op de plek waar dat cijfer staat. Als er in de rechterbovenhoek bijvoorbeeld een 3 staat, komt er in de derde van de negen lagen een 1. Als je alle lagen boven elkaar legt, onstaat er een soort kubusfiguur met een paar enen en veel nullen. Aan de hand van de hoogte van een 1 kan je bedenken welk getal dat in de soduku voorstelt.
Door de sudoku zo op te breken is het makkelijker om een programma te schrijven dat de regels van een sudoku checkt. Je kan nu voor elke laag een aantal eenvoudige voorwaarden bedenken, waardoor ze voldoen aan de regels van de sudoku. En je schrijft regels waar de lagen ten opzichte van elkaar aan moeten voldoen. Door de (voor een computer soms ingewikkelde) regels van een sudoku zo op te breken, ontstaat het algoritme. Er komt nog veel wiskunde bij kijken, maar het opbreken is één van de basisideeën waardoor dit concept werkt.
Meer toepassingen
Natuurlijk wordt een ingewikkeld algoritme zoals dit niet alleen gemaakt om een sudoku op te lossen. De onderzoekers denken dat hiermee binnenkort ook andere ingewikkelde problemen waarin configuratie een rol spreekt opgelost kunnen worden. Configuratie betekent hier de manier waarop iets in elkaar zit. Eiwitten bijvoorbeeld, de bouwstenen van het leven, bestaan vaak uit moleculen die op erg ingewikkelde wijze in en om elkaar heen zijn gedraaid. Met een algoritme zoals dit zou je ze kunnen ontknopen, en kunnen we meer leren over het leven.
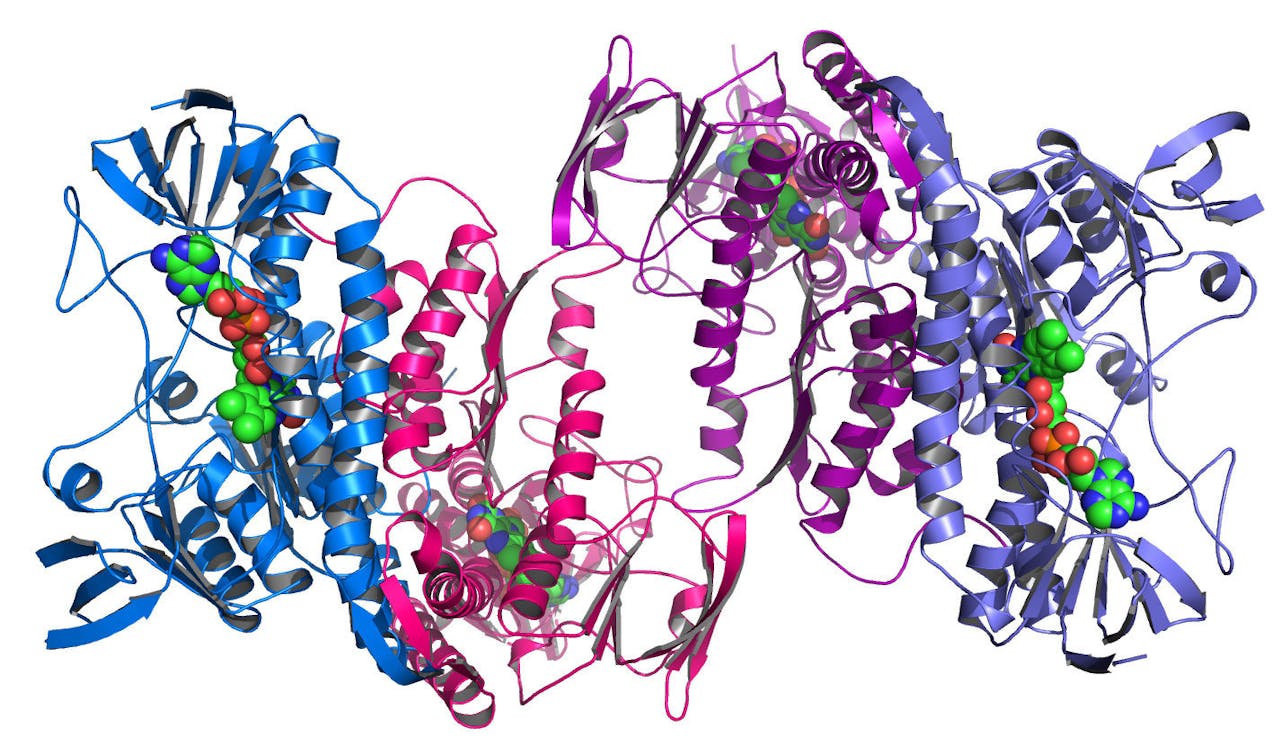
Een afbeelding van hoe een (in het echt heel kleine) eiwitketen eruitziet. Met het algoritme zou je de ingewikkelde, krullende vormen kunnen ontknopen.
Argonne National LaboratoryWat misschien nog wel interessanter is aan dit onderzoek, is de moeilijkheidsgraad van de sudoku. Zoltan Toroczkai en Maria Ercsey-Ravasz ontdekten dat de tijd die hun programma nodig had om een sudoku op te lossen overeenkwam met hoe moeilijk fanatieke sudoku-puzzelaars de puzzel vonden. Puzzels werden beoordeeld van 1 (makkelijk, één ster) tot 4 (extra moeilijk, vijf- of zes sterren). De onderzoekers berekenden eenzelfde soort getal, en het bleek dat moeilijke sudoku’s (die ook met een PC een lange tijd duren om op te lossen) een hoger getal kregen.
De moeilijkste sudoku die de onderzoekers vonden kreeg een getal van 3.6. Zo precies konden de puzzelaars het niet inschatten, maar het is wel grappig dat een computer met dit algoritme dezelfde dingen moeilijk vindt als een mens. Normaal is dat vaak niet zo: ‘gezichten herkennen’ is heel erg moeilijk om een computer aan te leren, terwijl mensen dit vaak al als baby kunnen.
Of het algoritme echt praktisch is om sudoku’s op te lossen is nog niet helemaal duidelijk. Voor het grootste gedeelte van de puzzels – zeker degene die in de kranten staan – voldoen de eenvoudigere oplossingsmachines op internet. Het feit dat dit algoritme niet alleen sudoku’s oplost, maar ook op andere manieren toepasbaar is, maakt het wel bijzonder. Maar waarschijnlijk vinden de meeste mensen het toch leuker om gewoon met pen en papier aan de slag te gaan en een sudoku met je hoofd op te lossen, in plaats van met hun computer.
Lees meer over sudoku’s op Kennislink:
Meer over sudoku’s op Wetenschap24:
- Patronen in een sudoku (Hoe?Zo! Radio, 2011)