Om de werking van een geneesmiddel te testen, zijn niet altijd grote groepen proefpersonen nodig. Mede dankzij Bayesiaanse statistiek kan elke individuele proefpersoon betrouwbare informatie opleveren. Onderzoekers van het Radboud UMC lieten zien dat zulke trials soms een volwaardig alternatief zijn voor de klassieke testmethode met grote groepen patiënten.
Mexiletine, een middel dat oorspronkelijk bedoeld is om hartritmestoornissen tegen te gaan, helpt ook om stijfheid en verkramping van spieren tegen te gaan bij mensen met de spierziekte niet-dystrofe myotonie. Dat blijkt uit een medische trial met 27 proefpersonen die onlangs gepubliceerd is in het vakblad JAMA.
Het belang van deze studie is een stuk breder dan de nieuwe toepassing van dit ene middel voor deze ene spierziekte. Dankzij een alternatieve aanpak, een zogeheten N-of-1 trial, leverde een test met slechts weinig proefpersonen toch een statistisch degelijk resultaat op. De N slaat hier op het aantal proefpersonen in een medische trial. Volgens Bas Stunnenberg, neuroloog aan het Radboud UMC en leider van dit onderzoek, maken N-of-1 trials het mogelijk om bij zowel individuele patiënten als bij groepen patiënten te bepalen of een behandeling echt werkt, en hoe goed die werkt.
Gouden standaard
Een van de dingen die echte geneeskunde onderscheidt van kwakzalverij en ‘alternatieve’ geneeskunde, is dat behandelingen volgens gestandaardiseerde methodes getest moeten worden om erkenning te krijgen. De gouden standaard voor erkenning is de randomized, double-blind, placebo controlled trial.
Deze houdt in dat je een grote groep patiënten op basis van toeval (randomized) in twee ongeveer even grote groepen verdeelt. De ene groep krijgt de behandeling of het geneesmiddel dat getest moet worden, de andere groep krijgt een placebo, een nepmiddel. Essentieel is dat noch de proefpersonen, noch de behandelend artsen weten wie het placebo krijgt, en wie het medicijn (double blind). Een veel voorkomende variant is dat een nieuwe behandeling vergeleken wordt met een al erkende behandeling, dus niet met een placebo, omdat het onaanvaardbaar kan zijn om ernstig zieke patiënten een middel te geven waarvan je al weet dat het niet werkt.
Na een vooraf vastgelegde behandelingsperiode wordt gemeten welke patiënten er nu beter aan toe zijn, en welke niet. Als er voldoende verschil is tussen de twee groepen, luidt de conclusie dat de behandeling werkt (of, als het verschil de verkeerde kant op wijst, dat de behandeling juist schadelijk is – ook dat komt voor). Maar wanneer is het verschil tussen de twee groepen voldoende?
Duizenden proefpersonen
Dat hangt van diverse factoren af, maar in het algemeen geldt: hoe kleiner het verschil in behandelingsresultaat tussen de twee groepen, hoe groter die groepen moeten zijn om een betrouwbare uitspraak te kunnen doen. Als een behandeling maar een klein verschil maakt – bijvoorbeeld: een gemiddeld iets langere levensduur voor kankerpatiënten – kunnen duizenden proefpersonen nodig zijn om enigszins betrouwbaar te beslissen of deze behandeling doet wat hij belooft. Dan ben je met zo’n trial al gauw jaren bezig en dat kost miljoenen euro’s.
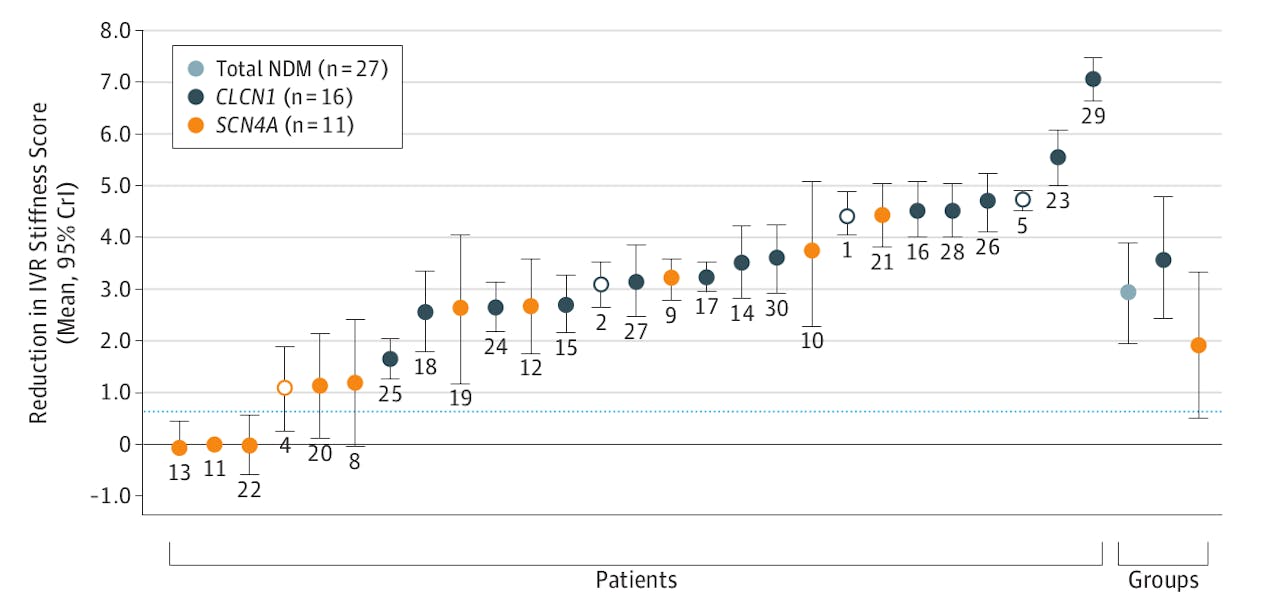
Het effect van de behandeling met mexiletine per proefpersoon, gerangschikt van geen of weinig effect naar veel effect. Elke proefpersoon kreeg vier weken lang mexiletine en vier weken een placebo, in een door toeval bepaalde volgorde. Ze werden onderscheiden wat betreft hun variant van het relevante gen, CLCN1 of SCN4A.
JAMA, Bas Stunnenberg e.a., Volume 320, Number 22De statistiek die hier wordt toegepast heet frequentistisch, en dit is in de geneeskunde verreweg de meest gebruikte benadering. Heel kort door de bocht geformuleerd: je gooit de data van elk van beide groepen in een bak en gaat die turven en middelen. De uitslag van zo’n test is voor niet-specialisten echter behoorlijk verwarrend. Formeel levert zo’n test namelijk niet meer op dan een p-waarde, bijvoorbeeld p=0,01. Dit betekent: de kans dat het geconstateerde verschil tussen de twee groepen proefpersonen slechts een toevallige uitschieter is, is 0,01, ofwel 1 procent.
Verwarrende p-waarde
Bij een p-waarde van 0,05 of kleiner is de gebruikelijke conclusie ‘dit is geen toeval’, en gaat men ervan uit dat de behandeling werkt. Maar dit is niet meer dan een wel/niet-uitspraak. Helpt dit nieuwe medicijn heel goed, of maar een beetje, en hoe zeker zijn we daarvan? Formeel zegt de p-waarde daar niets over. Een zeer lage p-waarde betekent niet per se dat een behandeling met grote zekerheid heel goed werkt, en het tegendeel geldt evenmin.
Een alternatief voor deze frequentistische statistiek is de Bayesiaanse statistiek. Net zo kort door de bocht geformuleerd: je doet vooraf een aanname over de kans dat de behandeling werkt, en elk snippertje informatie uit het onderzoek, per patiënt en per gebeurtenis, stelt die aanname naar boven of naar beneden bij. Als je aan het eind van de test alle informatie verwerkt hebt, kom je uit op een nieuwe, veel beter onderbouwde kans dat de behandeling werkt. Dat geeft ook de optie om voor slechts een deel van de patiënten, of zelfs maar één patiënt, die kans te berekenen.
Het heikele punt van de Bayesiaanse benadering is altijd de aanname vooraf: wat valt er voor zinnigs te zeggen over de kans dat een medicijn werkt, als het medicijn nog niet getest is? Ook daar valt wel een mouw aan te passen: je kunt de hele analyse meermaals doen, met heel verschillende aannames vooraf, en dan kijken hoe ‘gevoelig’ de eindconclusie is voor die aanname.
(In dit artikel op NEMO Kennislink vind je achtergrondinformatie over Bayesiaanse statistiek)
Kiezen is niet nodig
In het recente verleden kwamen ‘frequentisten’ en ‘Bayesianen’ nogal eens tegenover elkaar te staan, alsof het een kwestie was van goede en foute statistiek. Daarover schreven twee medisch statistici, Roger Lewis en Derek Angus, in december 2018 een commentaar in JAMA: ‘Dit is geen kwestie van frequentistisch versus Bayesiaans conclusies trekken; het is niet nodig om te kiezen.’
Zij hadden het in dit geval over een trial met een experimentele behandeling voor ernstige ademhalingsproblemen. Volgens de frequentische benadering leverde die nieuwe behandeling geen significant voordeel op, p was groter dan 0,05. Maar een Bayesiaanse heranalyse detecteerde wel degelijk een, weliswaar klein, voordeel voor de patiënt.
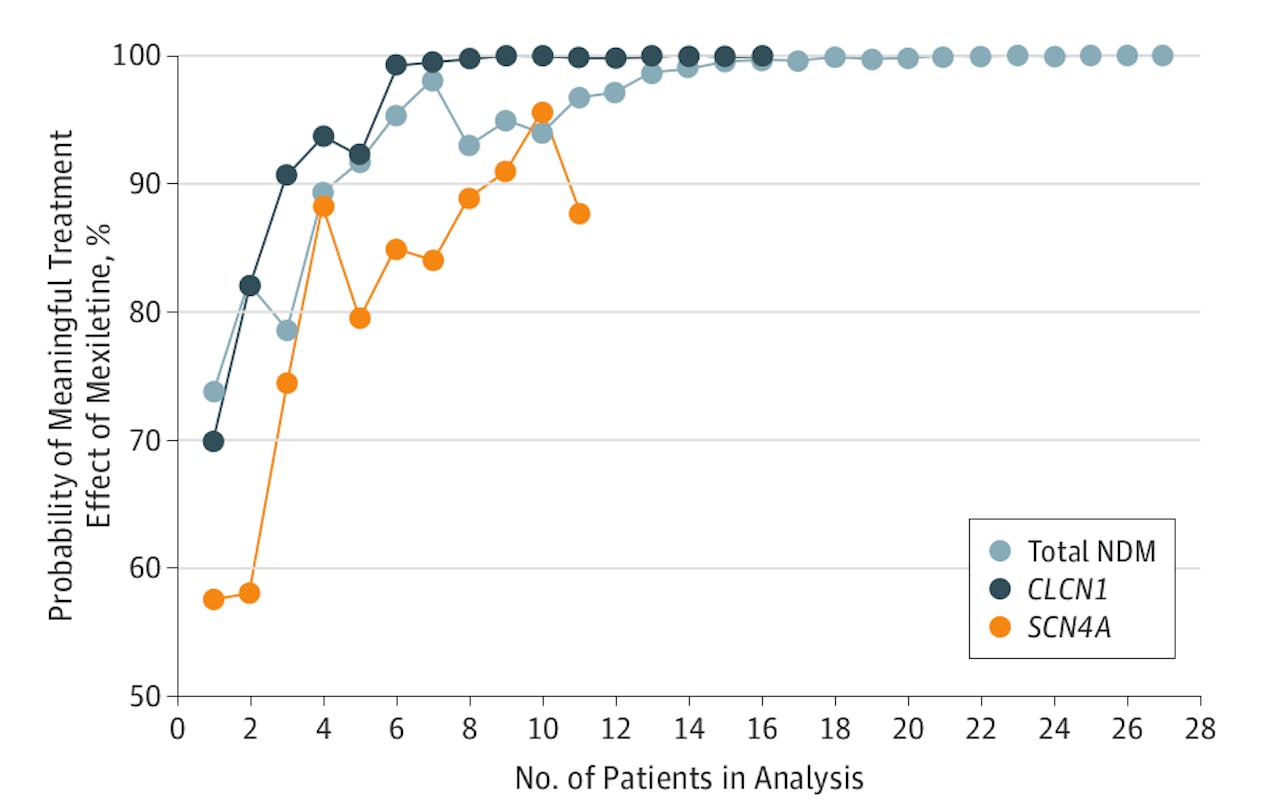
De kans dat mexiletine werkt, wordt beïnvloed door elke proefpersoon waarvan de resultaten verwerkt worden. Als iemand zich beter voelt bij toediening van mexiletine dan bij placebo, gaat de kans omhoog; bij een omgekeerd effect, gaat de kans omlaag (zoals bij proefpersoon 5 in de oranje groep). Al na 11 proefpersonen stijgt de kans van de groep als geheel boven de 95%, en is het effect volgens het klassieke criterium significant.
JAMA, Bas Stunnenberg e.a., Volume 320, Number 22In de trial van Stunnenberg en zijn collega’s vormde elk van de 27 patiënten als het ware z’n eigen controlegroep, omdat iedereen zowel vier weken lang mexiletine kreeg als vier weken lang een placebo, met een week ‘niets’ er tussenin (in een door toeval bepaalde volgorde). Een paar patiënten doorliepen deze cyclus twee keer.
Volgens de testopzet hadden de proefpersonen maximaal vier cycli kunnen doorlopen. Maar bij veel proefpersonen was het verschil in klachten tussen de placebo- en de mexiteline-periode zo groot, dat die volgens vooraf bepaalde criteria uit de trial genomen werden, en verder alleen nog behandeld met mexiteline.
Stunnenberg: “Dat is eigenlijk ongunstig voor de power (de statistische bewijskracht van de trial, red.), maar ethisch wel de juiste manier. Bij een minder sterk effect of vergelijking van meerdere middelen zou ik in het vervolg liever een vast aantal sets aanbieden (2-3). Maar dan heb je wel een grote kans dat patiënten bij een goed effect op een medicament uit de trial stappen, omdat ze niet nogmaals op een placebo en ander middel willen. Dit probleem hadden wij nu niet.”
Volgens de Bayesiaanse methode kon Stunnenberg nu van elke proefpersoon berekenen hoeveel effect mexiletine had, met een onderbouwde onzekerheidsmarge om die waarde heen. Op dezelfde manier kon ook het effect van mexiletine worden berekend op twee subgroepen proefpersonen, met twee varianten van het voor de ziekte relevante gen (zie afbeelding).
Speciaal voor zeldzame ziektes
Niet-dystrofe myotonie is een zeldzame erfelijke ziekte, dus 27 patiënten rekruteren voor zo’n trial is al heel wat. Omdat het effect van mexiletine heel duidelijk was, konden Stunnenberg en collega’s in dit geval de werkzaamheid ook volgens de gebruikelijke, frequentistische methode met slechts deze 27 patiënten aantonen. Stunnenberg: “Voordeel van onze analyse is wel dat we al na elf patiënten voldoende bewijs voor de werkzaamheid van mexiteline zien.”
N-of-1 trials zijn niet geschikt voor elk soort medicijn of behandeling. Bijvoorbeeld: het vergelijken van twee chirurgische behandelingen voor een gecompliceerde beenbreuk. Patiënten zouden er waarschijnlijk bezwaar tegen maken, als na de eerste behandeling hun andere been ook gebroken wordt om de alternatieve behandeling uit te testen.
Maar ze zijn bij uitstek geschikt om behandelingen voor zeldzame, chronische ziektes uit te testen. Stunnenberg stelt, dat de gebruikelijke route naar erkenning via een randomized controlled trial met een grote groep proefpersonen bij zulke ziektes vaak niet haalbaar is. Daardoor kunnen waardevolle behandelingen voor deze patiënten onterecht buiten bereik blijven.

