Grote netwerken op bijvoorbeeld social media als Facebook en Twitter worden al snel chaotisch. Toch kun je er mooie structuren in ontdekken, door een sociaal netwerk te zien als straten en steden.
Complexe netwerken vind je overal. Bijvoorbeeld in je brein, op het internet en op sociale media. Of neem een communicatienetwerk zoals het telefoonnetwerk van België (hieronder links te zien). Punten hierin zijn Belgen, en er is een lijn tussen twee perosonen als ze elkaar ooit een keer gebeld hebben.
Het is meteen duidelijk dat België verdeeld is in een Franstalig en Vlaams deel. Onderling bellen ze vaak. Tussen de twee groepen zijn maar weinig lijnen, wat niet zo gek is gezien de taalbarrière. Maar ook landen waarbij dit geen rol speelt, kunnen verdeeld zijn in groepen. In het telefoonnetwerk van Groot-Brittanië (rechts) zijn vergelijkbare structuren te zien. Mensen uit dezelfde provincie bellen elkaar veel vaker dan personen uit andere provincies. Londen verbindt wel alle groepen in het telefoonnetwerk met elkaar.
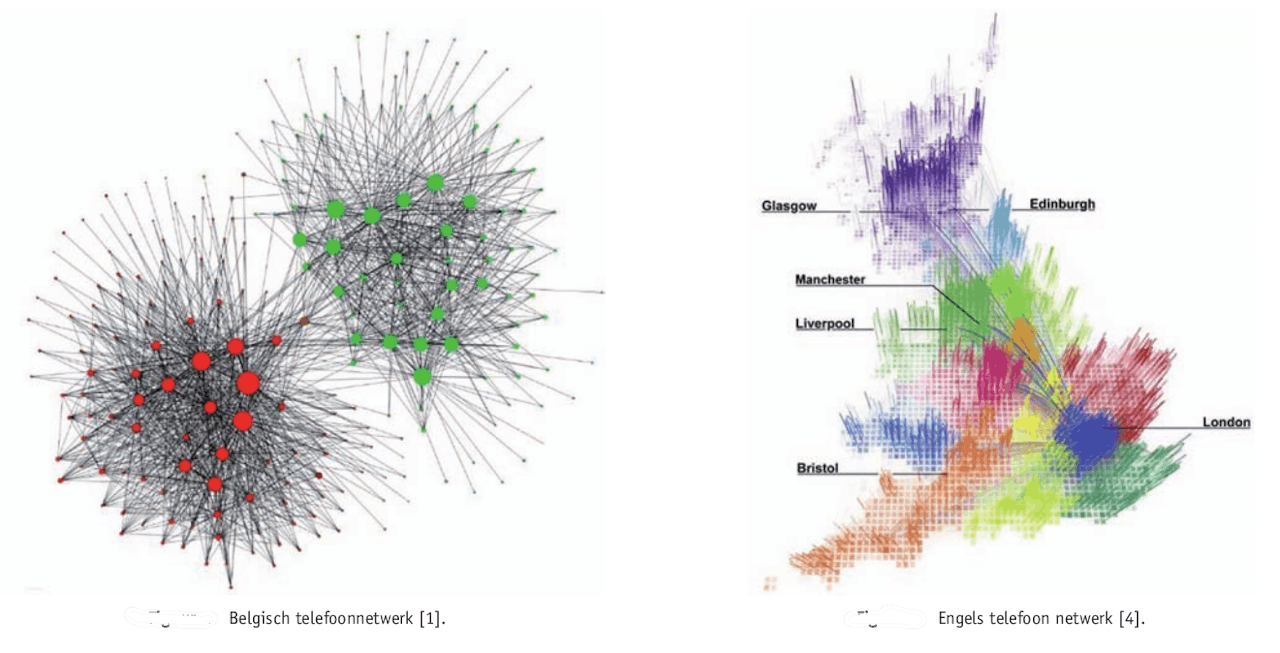
Schema van welke gebruikers via de telefoon contact met elkaar gehad hebben. Het Belgische telefoonnetwerk, links, vertoont een duidelijke taalbarriere. In het telefoonnetwerk van Groot-Brittannie is Londen een hub die alle provincies met elkaar verbindt.
Ratti et al; Vincent Blondel.Het is interessant dat in heel andere netwerken vergelijkbare groepsstructuren opduiken. Hieronder (links) zie je bijvoorbeeld een plaatje van mijn LinkedIn-netwerk. Punten zijn mijn connecties, en een lijn betekent dat twee van mijn vrienden ook met elkaar bevriend zijn. Op het eerste gezicht lijkt dit een grote chaos. Toch zien we in het plaatje rechts dat het netwerk verborgen groepsstructuren bevat.
Maar hoe kun je deze groepsstructuren wiskundig uit de chaos van het vorige plaatje halen? Dit is een moeilijke vraag waar onder andere wiskundigen, natuurkundigen en informatici zich het afgelopen decennium over hebben gebogen. Het vinden van deze verborgen groepsstructuren heeft ook veel praktische toepassingen, doordat groepsstructuren in allerlei verschillende soorten netwerken voorkomen. Je kunt bijvoorbeeld denken aan adverteerders in sociale netwerken die zich willen richten op bepaalde groepen van mensen met dezelfde interesses of woonplaats.

Om te ontdekken waar de groepen zich in een netwerk bevinden, moet eerst duidelijk zijn wat een groep precies is. Als we naar de bovenstaande plaatjes kijken, is het intuïtief duidelijk dat een groep aan twee eigenschappen voldoet: er zijn relatief veel verbindingen tussen punten in dezelfde groep of er zijn relatief weinig verbindingen tussen punten in verschillende groepen.
Een kaart van het netwerk
Er zijn in de loop der tijd diverse methoden ontwikkeld om groepen in een netwerk te identificeren. Een recent voorbeeld is de Infomap. Deze bekijkt een willekeurige wandeling over het netwerk: een persoon die van punt naar punt over de lijnen van het netwerk loopt. In ieder punt kiest hij telkens met gelijke kans een van de buren om naar toe te gaan. Als een netwerk groepsstructuren bevat, dan verwacht je dat deze willekeurige wandelaar relatief veel tijd doorbrengt binnen een groep voordat hij deze verlaat, omdat groepen relatief veel lijnen bevatten. Tussen de verschillende groepen zijn veel minder lijnen, de wandelaar zal dus niet zo vaak van groep naar groep bewegen. Maar hoe gebruik je deze intuïtie om de groepsstructuren te ontdekken?
Stel dat je in woorden wil beschrijven hoe een willekeurige wandelaar zich door het netwerk heen beweegt. Om dit te doen, moet je ieder punt in het netwerk een naam geven. Je beschrijft bij elke stap de naam van het punt waar de wandelaar zich naartoe beweegt. In een groot netwerk heb je dan veel verschillende namen nodig.
Een slimmere manier om de route te beschrijven is zoals een route op een kaart. Niet alle straten in Nederland hebben een unieke naam, er zijn verschillende Stationsstraten in Nederland. Maar binnen een bepaalde stad zijn straatnamen natuurlijk wel uniek. Als je een route door Nederland beschrijft, dan zul je waarschijnlijk de straatnamen gebruiken van de stad waar je nu bent. Alleen als je naar een andere stad gaat, gebruik je de naam van die andere stad. In een netwerkperspectief zijn we dus eigenlijk op zoek naar de steden en dorpen in het netwerk: gebieden met veel straten.
De beschrijving van een wandeling
Stel dat we binaire namen geven aan punten in een netwerk dat is opgedeeld in groepen. Binair wil zeggen: we nummeren de punten, waarbij we alleen de cijfers 0 en 1 gebruiken. Namen binnen een groep moeten uniek zijn. Als een groep veel punten bevat, worden de binaire namen van punten in die groep dus erg lang (als je honderd straten binair nummert, heb je al zes cijfers per naam nodig, want dan zijn er maar 128 mogelijke namen, van 000000 tot 111111). Alle groepen hebben ook een unieke binaire naam (dit zijn de ‘steden’).
We beschrijven de route van de willekeurige wandelaar door steeds de naam van het punt te noemen waar hij naartoe gaat. Als de willekeurige wandelaaar van groep wisselt, moeten we daarnaast de naam van de nieuwe groep opschrijven. De beschrijving wordt dus erg lang als de wandelaar vaak van groep verandert, omdat we steeds zowel de naam van het punt waar diegene naartoe gaat, als de bijbehorende groepsnaam moeten opschrijven. De beschrijving wordt juist kort als we groepen hebben waar de wandelaar lang in blijft rondlopen. Als we de groepen te groot maken, wordt de beschrijving juist weer erg lang, omdat de unieke binaire namen van de punten dan erg lang worden. De vraag is dan: wat is de opdeling in groepen die de beschrijving van de willekeurige wandeling zo kort mogelijk maakt?
Overlappende groepen
Dit komt neer op het minimaliseren van een wiskundige vergelijking, de zogeheten Map Equation, die telt hoeveel binaire getallen gemiddeld nodig zijn voor een stap van de willekeurige wandelaar, afhankelijk van de gekozen opdeling in groepen. De opdeling die deze vergelijking minimaliseert, maakt de beschrijving van de wandeling het kortst, en dat is de opdeling die het netwerk het meest efficiënt in ‘steden’ opdeelt. Hieronder zien we hoe de Infomap-methode erin slaagt om de groepsstructuren in het netwerk te ontdekken.
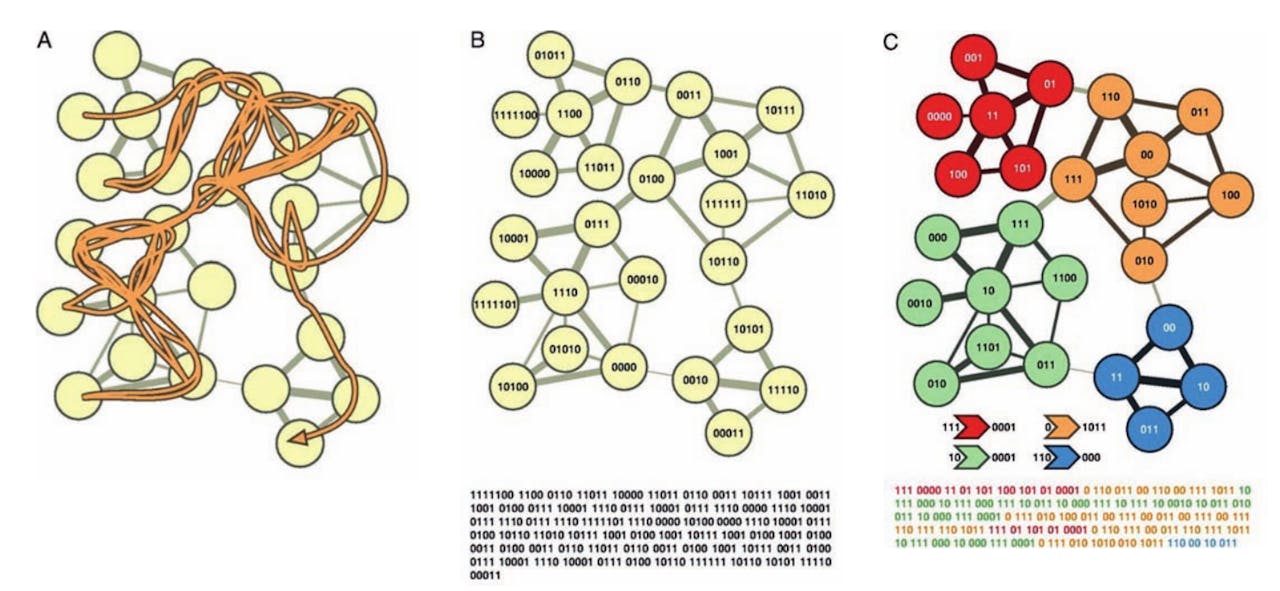
(a)Om een groot netwerk onbevooroordeeld te analyseren, is het vaak het beste om er random – aangestuurd door een dobbelsteen – doorheen te lopen. (b) De binaire beschrijving van de random wandeling zonder groepsstructuren mee te nemen (c ) De binaire beschrijving van de random wandelling opgedeeld in groepen is een stuk korter.
Martin RosvallMaar er zijn nog een hele hoop problemen op dit gebied op te lossen. Op sociale netwerken horen de meeste mensen bijvoorbeeld thuis in verschillende groepen: familie, sportvrienden en collega’s bijvoorbeeld. In dit soort netwerken is het dus helemaal niet mogelijk is om iedereen aan één bepaalde groep toe te wijzen omdat de groepsstructuren in sociale netwerken elkaar vaak overlappen. Om bijvoorbeeld groepsstructuren te vinden die mensen op sociale media indelen op basis van hun interesses, heb je dus een methode nodig die overlappende groepsstructuren vindt. De methode die hierboven beschreven staat kan, net als diverse andere methodes, deze overlappende groepen niet vinden. Kortom, het probleem van groepen vinden in netwerken is nog lang niet opgelost.

