Het ‘zwakke’ vermoeden van Goldbach is na 227 jaar bewezen. Een wiskundige van het École Normale Supérieure in Parijs heeft laten zien dat elk oneven getal te schrijven is als drie priemgetallen.
De exacte formulering van het zwakke vermoeden van Goldbach luidt dat elk oneven getal groter dan vijf geschreven kan worden als een som van drie priemgetallen. Zo is 31 te schrijven als 7+11+13. De stelling is simpel, maar het bewijs niet. De op het open acces-publicatienetwerk arXiv verschenen publicatie van H. A. Helfgott, waarin het bewijs uit de doeken wordt gedaan, telt maar liefst 133 pagina’s.

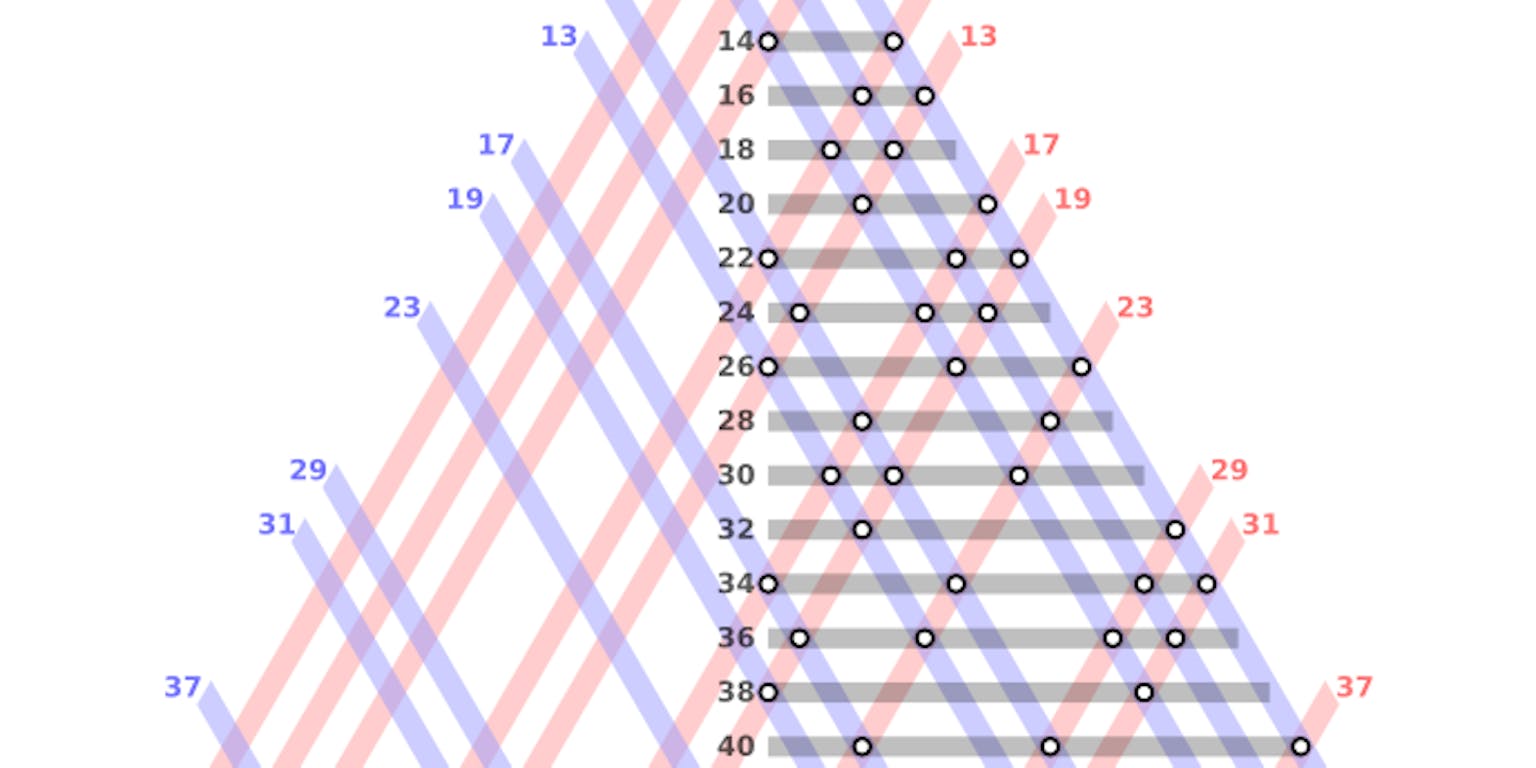
Een grafische weergave van het Goldbach-vermoeden voor éven getallen. In het zwart staan alle even getallen tussen 4 en 50. De lijnen en witte stippen geven aan hoe een getal te schrijven is als een som van twee priemgetallen.
Adam Cunningham and John Ringland, Wikimedia CommonsDe publicatie bewijst de stelling voor oneven getallen groter dan 10^30, omdat – zoals Helfgott aangeeft – voor alle getallen kleiner dan 10^30 al met de computer gecheckt is dat de stelling klopt. Natuurlijk is Helfgotts bewijs veel beter dan een berekening met de pc, omdat het geldt voor álle getallen, tot in het oneindige.
Het echte vermoeden van Goldbach zegt dat elk getal te schrijven is als de som van twee priemgetallen. Dit is een ‘sterkere’ wiskundige stelling dan wat er nu bewezen is, omdat áls het echte vermoeden waar is, dan is het zwakke vermoeden waar. Immers, als elk getal als twee priemgetallen te schrijven is, dan kan elk oneven getal als drie priemgetallen geschreven worden, door gewoon drie op te tellen bij een even getal. Zo is het sterke vermoeden waar voor 12 (te schrijven als 7 + 5), en is dus het zwakke vermoeden waar voor 15.
De afgelopen jaren kwam een bewijs voor het oneven vermoeden steeds dichterbij. De beroemde wiskundige Terence Tao bewees al dat elk oneven getal te schrijven was als de som van vijf priemgetallen. Nu heeft Helfgott eindelijk het vermoeden bewezen voor drie priemgetallen. Officieel moet zijn bewijs nog worden goedgekeurd door andere wiskundigen, maar het lijkt erop dat Helfgotts resultaat klopt; ook Terence Tao denkt dat alles correct is.
De ontdekking kwam heel toevallig op dezelfde dag naar buiten als het nieuws dat er een oneindige hoeveelheid priemduo’s zijn die minder dan een paar miljoen van elkaar liggen. Daar komt nog bij dat het tweelingpriemvermoeden en het vermoeden van Goldbach allebei al erg lang onbewezen zijn en waarschijnlijk even moeilijk te bewijzen zijn. In die zin lijken ze dus ook nog eens erg op elkaar.