De familie van de veelvlakken, bekend van de kubus en de piramide, heeft er een zusje bijgekregen: het Goldberg-veelvlak. En dat is bijzonder, want de laatste gezinsuitbreiding was 400 jaar terug. Psychologen van de Universiteit van Californië ontdekten de nieuwe soort veelvlakken.
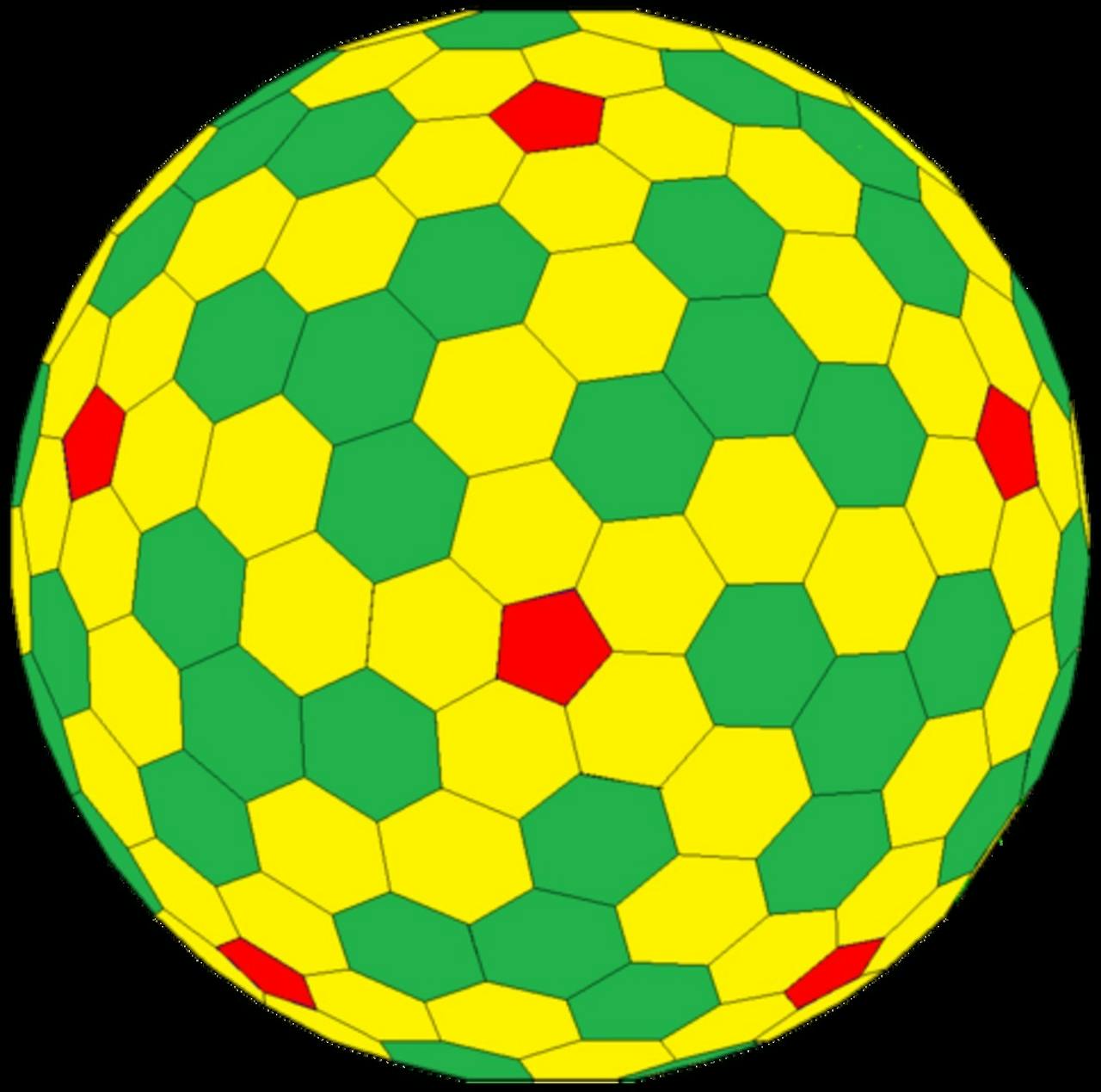
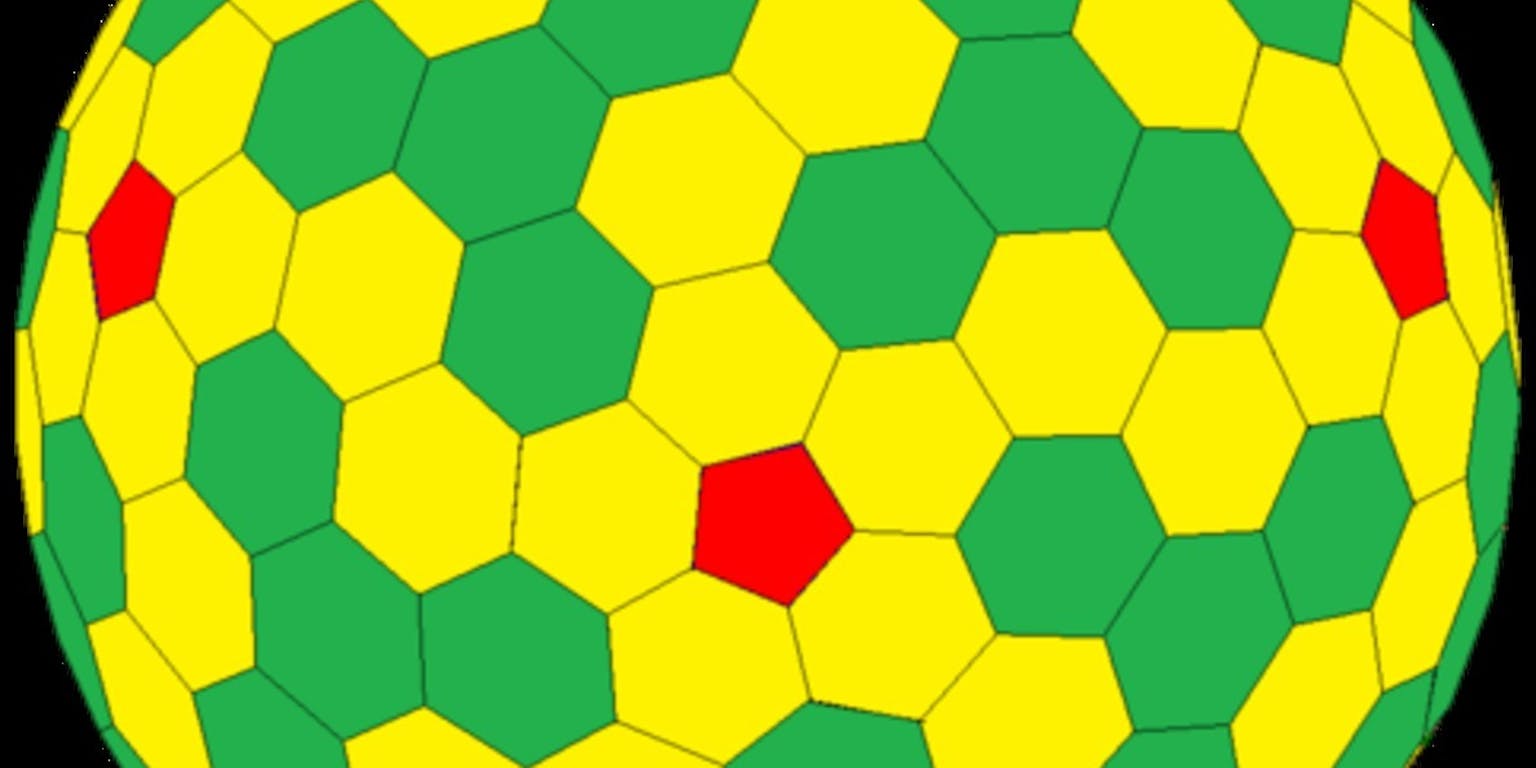
Dit is een voorbeeld van de nieuwe categorie veelvlak. Het lijkt wel een bol, maar hij bestaat simpelweg heel veel platte vlakken waardoor de figuur steeds minder hoekig wordt – net als bij een voetbal. De verschillende kleurtjes staan voor verschillende figuren.
The ConversationMisschien ken je ze van de meetkunde op school: ingewikkelde 3d-figuren waarvan de zijden een regelmatig patroon vormen, zoals bijvoorbeeld de tetraëder: een piramide die uit louter driehoek bestaat. Deze is, samen met de drie andere bekende veelvlakken, onderdeel van de Platonische veelvlakken. Er zijn nog twee veelvlakgroepen, maar sinds de zeventiende eeuw is er weinig spannends meer bijgekomen in de wereld van 3d-figuren.
Nu hebben de onderzoekers echter naar eigen zeggen een hele nieuwe categorie van veelvlakken ontdekt, die bovendien uit te breiden is zo lang als je wilt.
Inspiratie voor hun vreemde vorm kwam van de wiskundige Michael Goldberg (niet te verwarren met Goldbach, die een beroemd vermoeden heeft) die een aantal Goldberg-veelvlakken bedacht. Deze veelvlakken bleken echter geen veelvlakken in de strikte wiskundige zin van het woord, omdat de onderdelen van het veelvlak niet altijd ‘plat’ waren; er zat soms een kleine bolling in de figuur. Voor meetkundigen kwalificeert een figuur zich daardoor niet als regelmatig veelvlak.
De andere veelvlakken
Een nieuw ontdekte veelvlakgroep is niet niks, maar kende je de bekende veelvlakgroepen al? Even een korte (her)introductie:
Platonische veelvlakken zijn de bekendste. Onder andere de kubus valt in de deze groep, net als de dodecaëder en de isocaëder. Ze voldoen aan drie regels: alle zijden zijn hetzelfde (dus driehoeken, vierkanten, vijfhoeken enzovoort); de zijden raken elkaar alleen in de ribben an de figuur; ze doorkruizen elkaar dus niet; elk hoekpunt van de figuur is een ontmoetingspunt voor evenveel vlakken. Aan deze regels voldoen vijf figuren.
Bij de Archimedische veelvlakken, waarvan er dertien zijn, hoeven niet alle zijden van de figuur hetzelfde te zijn. Zo kan je dus een figuur hebben waarvan zes zijden vierkanten zijn en de rest zeshoeken. Deze figuren zien er meteen ‘raar’ uit ten opzichte van de keurige Platonische veelvlakken.
De Kepler-veelvlakken krijg je door de zijden van een gewoon veelvlak te ‘versterren’; op een systematische manier rek je elk vlak uit tot een platte stervorm. Zo ontstaat een 3d-ster, die vanaf de voorkant vijfhoeken als voorkant lijkt te hebben. Ze zijn alweer exotischer en ingewikkelder te maken dan de Archimedische veelvlakken.
De drie andere categorieën. Van links naar rechts: Platonische veelvlakken, regelmatig en orderlijk; Archimediaanse veelvlakken, al chaotischer omdat ze twee verschillende soorten zijden kunnen hebben; Kepler-veelvlakken, die door de ‘versterring’ van gewone veelvlakken een opvallend en chaotisch uiterlijk krijgen.
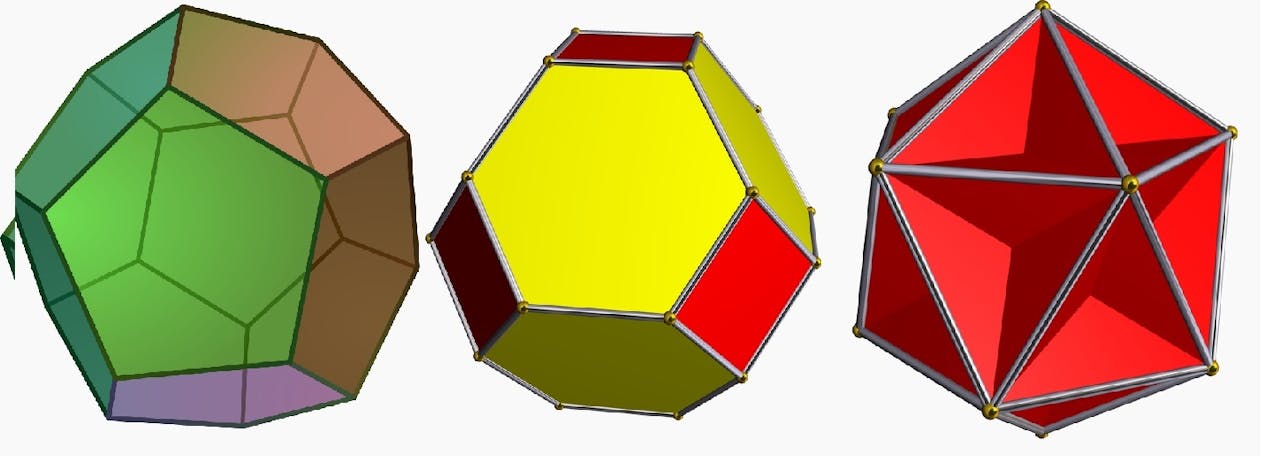
De twee onderzoekers vroegen zich vervolgens af hoe je Goldbergs figuren dan wél tot regelmatige veelvlakken kan maken. Daarvoor moesten ze nogal wat uitvogelen. Simpel gezegd: ze begonnen met een kubus en ‘bliezen die op’. Daardoor gaan de zijden van de kubus vol staan. Vervolgens moesten ze de bolle gedeelten zo opbreken, dat het hele bolle vlak uit (platte) veelhoeken bestaat. Na wat gepuzzel lukte het ze om zo’n figuur te maken, die niet thuishoorde in de andere veelvlak-families.
En ze gingen nog verder in hun idee: door niet een kubus, maar een andere driedimensionale figuur ‘op te blazen’ kan je nog veel meer van deze nieuwe veelvlakken maken. Sterker nog, omdat je telkens maar zijden aan de beginfiguur kan toevoegen kan je zelfs oneindig veel veelvlakken maken.
Dat is bijzonder, omdat er in de categorieën die bestonden altijd maar een eindig aantal figuren bestond. Dat die barriere nu weg lijkt te vallen is niet alleen voor de meetkunde-fanaat interessant. Er kunnen ook directe toepassingen zijn. In de architectuur bijvoorbeeld kunnen de veelvlakken als inspiratie voor een bouwwerk dienen. Maar ook de natuur blijkt verrassend vaak de nieuwe soort veelvlakken te gebruiken. Onder een microscoop heeft een virus bijvoorbeeld de vorm van een ‘opgeblazen kubus’ met platte veelvlakken. Begrijpen hoe een virus eruitziet en wat daarachter voor mechanisme steekt, kan helpen om het virus beter te bestrijden.