Naar de content

Leep landmeten

Eerste hulp bij de Wetenschapsquiz 2018

Pixabay, Arnaud Liégeois via CC0

De traditionele VPRO Wetenschapsquiz bevat altijd een wiskundeopgave. Dit jaar gaat die over het eerlijk verdelen van drie even grote kavels land. We helpen je op weg om grip te krijgen op dit schijnbaar onoverzichtelijke probleem. Uiteraard zonder de oplossing weg te geven.

11 december 2018
De opgave

Vraag 11: Vijf boeren moeten drie kavels land van elk 1 hectare groot eerlijk verdelen. Iedere boer krijgt dus 0,6 hectare land. Niemand vindt het een probleem als zijn grond uit meerdere stukken bestaat, mits elk stuk minstens 0,25 hectare groot is. Lukt het om de kavels onder deze voorwaarde te verdelen?

a: Nee, het kleinste stuk is altijd kleiner dan 0,25 hectare.

b: Ja, dat lukt net.

c: Ja, het kleinste stuk kan zelfs groter dan 0,25 hectare zijn.

Zonder de eis dat het kleinste stuk land minstens 0,25 hectare groot is, zou de opgave triviaal zijn. Er zijn dan ontelbare oplossingen; een simpele verdeling is bijvoorbeeld: geef boer 1, 2 en 3 elk 0,6 hectare van kavel A, B en C. Geef boer 4 de resterende 0,4 hectare van kavel A en de helft van het restant van kavel B (0,2 hectare), en geef boer 5 de andere helft van het restant van kavel B (0,2) en het restant van C (0,4).
Maar deze verdeling bevat twee stukken die kleiner zijn dan 0,25 hectare, en is dus ongeldig.

Je kunt nu driftig andere verdelingen gaan uitproberen, maar dat kon wel eens heel lang gaan duren. En als je geen geldige verdeling vindt, bewijst dat natuurlijk nog niet dat die niet bestaat. En stel, je vindt een verdeling waarin het kleinste stuk precies 0,25 hectare is: dat is nog geen bewijs, dat er geen verdelingen bestaan met een kleinste stuk groter dan 0,25 hectare.

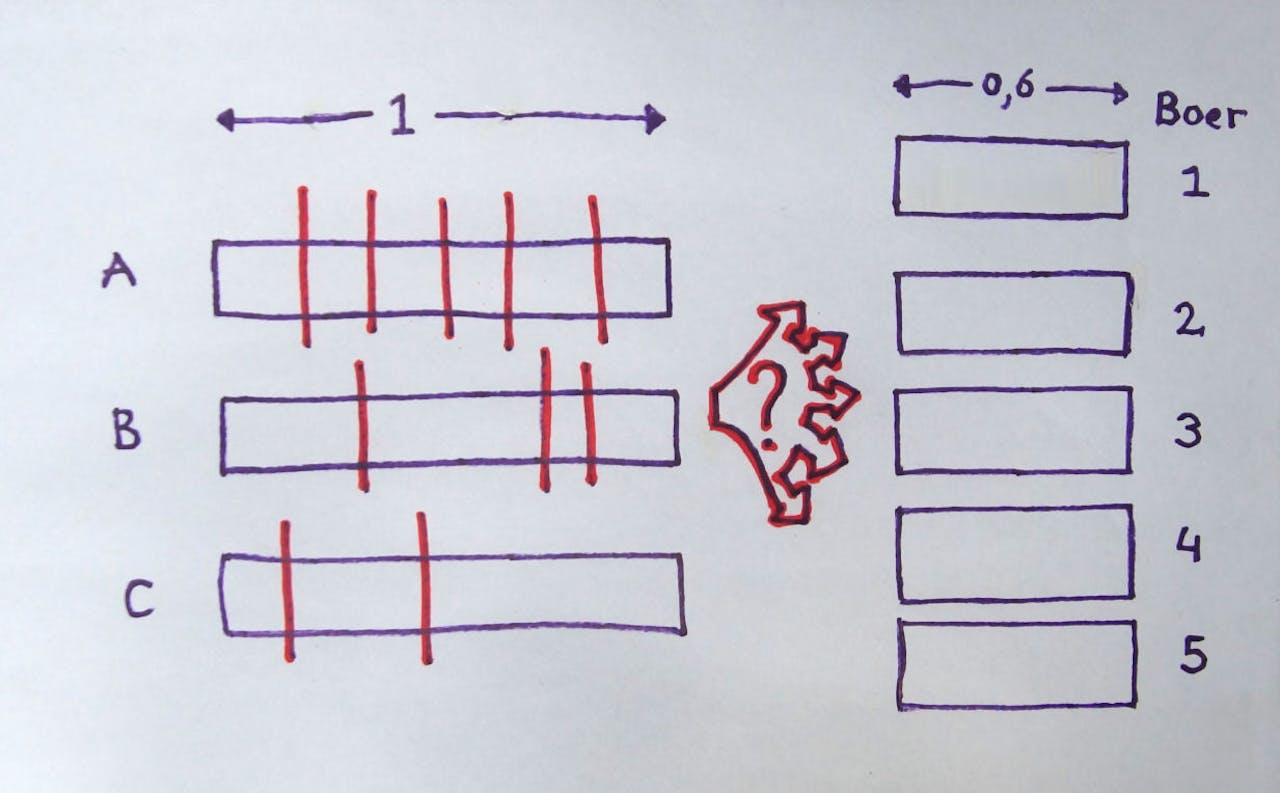
Omdat de opgave niets zegt over de vorm van de drie kavels A, B en C, mag je aannemen dat dit langwerpige stroken land zijn waar je stukken vanaf ‘knipt’ om ze onder de vijf boeren te verdelen. Zo reduceer je het probleem van twee dimensies (vlakverdelingen) naar één dimensie (getallen opdelen en optellen). Het afgebeelde voorbeeld is willekeurig, het is niet de oplossing.

Arnout Jaspers

In plaats van lukraak uitproberen, gaan we daarom een redenatie opzetten die ons dichter bij het antwoord brengt.
Vraag je eerst eens af uit hoeveel stukken het land van een boer kan bestaan – áls een geldige verdeling mogelijk is. De bovengrens is al heel simpel: elk stuk moet minimaal 0,25 hectare zijn, en een boer heeft in totaal maar 0,6 hectare. Zijn land bestaat dus uit minder dan drie stukken, want 3 × 0,25 = 0,75 > 0,6.

Conclusie I: het land van elke boer bestaat uit één of twee stukken.

Maar is het wel mogelijk, dat het land van een boer uit één stuk bestaat?
Dat stuk van 0,6 hectare is dan in zijn geheel afkomstig uit een van de drie kavels, zeg kavel A. Dan blijft van kavel A 0,4 hectare over. Kan je een stuk van 0,4 hectare in zijn geheel aan een andere boer kwijt? Als dit stuk naar een andere boer gaat, heeft die nog recht op 0,6 – 0,4 = 0,2 hectare land. Maar in een geldige verdeling kun je een stuk van kleiner dan 0,25 hectare nooit opvullen.
Dus: je kunt het restant van 0,4 hectare niet in z’n geheel aan een andere boer geven. Maar het kan ook niet in twee (of meer) stukken naar andere boeren gaan, want dan is minstens een van beide stukken kleiner dan 0,25 hectare (immers, 2 × 0,25 > 0,4).

Conclusie II: het land van een boer kan niet uit één stuk bestaan.

Conclusie I + II: elke boer heeft precies twee stukken land.

Anders geformuleerd: de drie kavels moeten in tien stukken verdeeld worden. Op het eerst gezicht lijken we niet veel opgeschoten, want we weten nog niets over de groottes van deze stukken. Het aantal mogelijkheden lijkt eindeloos. Maar als je nadenkt over hoeveel stukken land elk van de kavels kan leveren, blijkt het aantal mogelijkheden verrassend klein.

Pixabay, Arnaud Liégeois via CC0

(toegevoegd na de uitzending van de Wetenschapsquiz op 29 december:)
Want hoe kunnen drie kavels in totaal tien stukken land opleveren? En verdeling als 8-1-1 of 5-3-2 is onmogelijk, want dan zou minstens één stuk van de kavel die in achten of vijfen wordt verdeeld, kleiner zijn dan 0,25 hectare. Een kavel kan hoogstens in vier stukken verdeeld worden, en dan zijn alle stukken ook precies 0,25 hectare.

En met een verdeling waarbij alle kavels in minder dan vier stukken verdeeld worden, kom je niet aan tien stukken; het maximum is negen, met de verdeling 3-3-3.

Alleen de verdelingen 4-4-2 en 4-3-3 leveren tien stukken op die allemaal minstens 0,25 hectare groot zijn. Maar kan de verdeling 4-4-2 wel? Deze bevat acht stukken van 0,25 hectare. Maar dan moeten er boeren zijn met alleen maar twee stukken van 0,25 hectare, en dat kan niet, want dan komen ze niet aan 0,6 hectare.

Zo blijft alleen de verdeling 4-3-3 over. Er zijn dan vier boeren die een stuk van 0,25 hectare krijgen. Hun tweede stuk is dus 0,6 – 0,25 = 0,35 hectare. Dus er zijn vier stukken van 0,35 hectare. Omat je een kavel van 1 hectare niet volledig kunt opdelen in stukken van 0,35 hectare, moeten er twee kavels zijn die elk twee stukken van 0,35 hectare leveren. Die twee kavels bestaan dus uit elk uit drie stukken van 0,35 , 0,35 en 0,3 hectare, en de vier stukken van 0,25 komen uit de derde kavel.

Zo wordt de verdeling:

Vier boeren krijgen elk 0,35 + 0,25, de vijfde boer krijgt 0,3 + 0,3.

Het goede antwoord op vraag 11 van de Wetenschapsquiz is dus b.

PS: Deze vraag is ontleend aan een algemener wiskundig pobleem, het muffin probleem. Een artikel hierover verscheen in september 2018 in NRC Handelsblad.

ReactiesReageer