Voor zover bekend heeft het geen nut, maar duizenden liefhebbers zoeken naar extreem grote priemgetallen (getallen zonder delers). Op 3 januari 2018 kwam de bevestiging dat het vijftigste Mersenne-priemgetal gevonden is, door een computer van Jonathan Pace in de Verenigde Staten. Hij draait mee in de Great Internet Mersenne Prime Search (GIMPS).
Priemgetallen – gehele getallen die door geen enkel getal deelbaar zijn – hebben wiskundigen altijd gefascineerd. Het zijn in zekere zin de atomen van de rekenkunde; immers, uit de priemgetallen (2, 3, 5, 7, 11, 13, 17, 19, 23…) kun je door vermenigvuldiging alle overige gehele getallen maken. Er is nog nooit een deterministisch patroon ontdekt in hoe ze verspreid liggen tussen de overige getallen. Ook bestaat er, voor zover bekend, geen formule die alleen maar priemgetallen oplevert.
Daarom is het zoeken naar grote priemgetallen nog steeds iets wat veel wiskundigen en liefhebbers bezighoudt. De afgelopen twintig jaar heeft de Great Internet Mersenne Prime Search (GIMPS) telkens de nieuwe recordhouders geleverd. GIMPS omvat gratis downloadbare software die momenteel op duizenden computers naar nieuwe priemgetallen zoekt in de tijd dat ze stand-by staan. De nieuwste aanwinst, M77232917, een priemgetal van 23.249.425 decimale cijfers, is eind vorig jaar gevonden door een computer van Jonathan Pace, een 51 jaar oude elektrotechnisch ingenieur uit Germantown, Tennessee (Verenigde Staten).
Viervoudig gecheckt
Vervolgens is zijn claim op vier andere computersystemen geverifieerd, om uit te sluiten dat het hier om een computerbug gaat. Op 3 januari 2018 kwam de bevestiging dat M77232917 echt een priemgetal is. Pace deed al veertien jaar mee met GIMPS, en wint nu een prijs van drieduizend dollar voor zijn ontdekking.
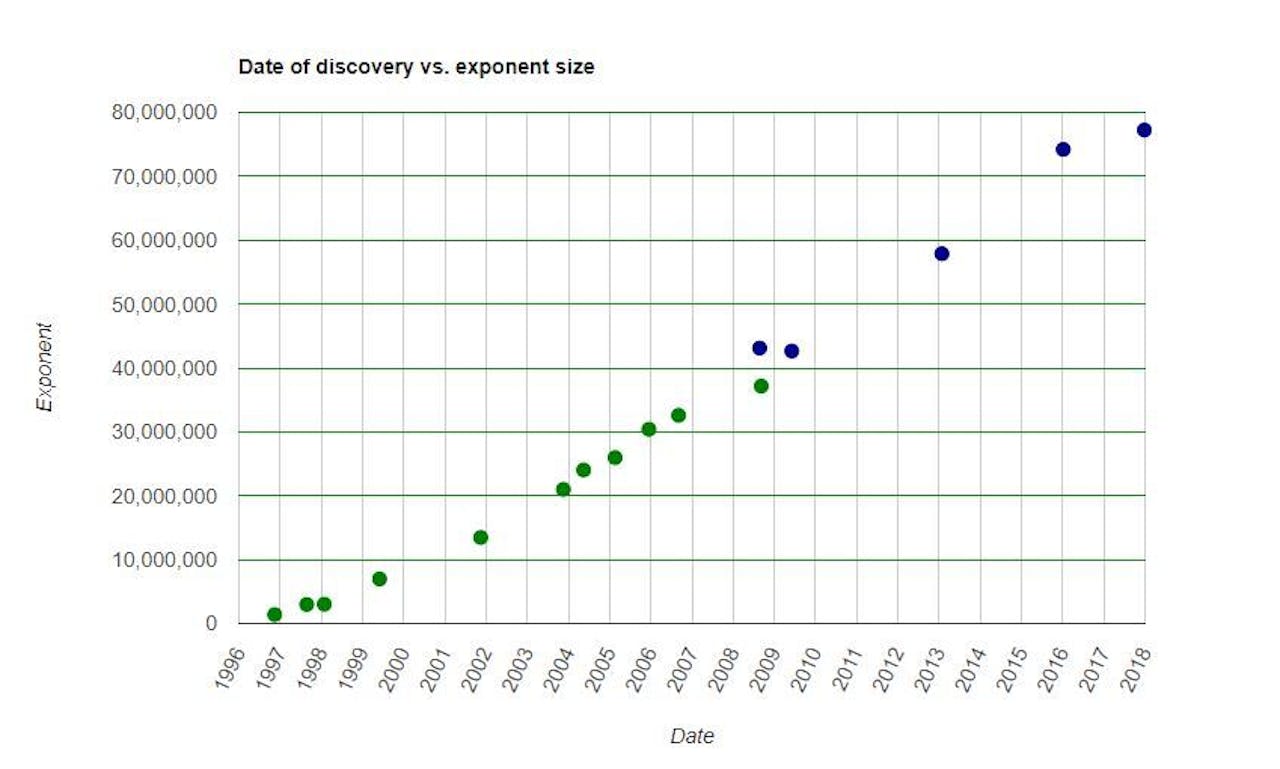
De voortgang van de jacht op Mersenne-priemgetallen. Verticaal staat de exponent N van het Mersenne-priemgetal, dat altijd van de vorm 2N – 1 is.
GIMPSSteeds grotere Mersenne-getallen zijn heel makkelijk te maken en hebben allemaal dezelfde vorm: 2N – 1. In woorden: vermenigvuldig N getallen 2 met elkaar, en trek daar 1 vanaf. Als je een Mersenne-getal wilt vinden dat priem is, moet de exponent N in ieder geval priem zijn. De nu gevonden recordhouder M77232917 is 277.232.917 – 1, en inderdaad is 77.232.917 zelf ook een priemgetal.
Het is voor een computer een koud kunstje om zulke priemgetallen N van acht – of negen, of tien – cijfers te vinden. Maar het probleem is: dit is geen garantie dat het bijbehorende Mersenne-getal ook priem is. Dat zul je apart moeten checken, en omdat een Mersenne-getal met exponent N veel en veel groter is dan N zelf, duurt dit veel langer. En bijna altijd blijkt het Mersenne-getal dan toch geen priemgetal te zijn.
Efficiënte test
Niettemin beperkt de zoektocht naar extreem grote priemgetallen zich al decennia tot Mersenne-getallen, omdat er een redelijk snelle, efficiënte priemgetaltest bestaat, de Lucas-Lehmertest, die alleen voor Mersenne-getallen werkt. Voor een willekeurig getal van miljoenen cijfers is het ook voor de snelste computers onbegonnen werk om te testen of dit een priemgetal is.
Er is niet te voorspellen of een Mersenne-getal priem is, en de Great Internet Mersenne Prime Search houdt dus in, dat duizenden vrijwilligers en hun computers van zoveel mogelijk Mersenne-getallen checken of ze de begeerde eigenschap hebben. Het is dan ook puur toeval dat juist de computer van Price het vijftigste Mersenne-priemgetal vond.
Overigens is nog niet helemaal zeker dat dit ook qua grootte het vijftigste Mersenne-priemgetal is. Tussen N = 37.156.667 (de exponent van het 45ste Mersenne priemgetal) en de N = 77.232.917 van deze nieuwe recordhouder liggen ruim twee miljoen priemgetallen, waarvoor nog niet in alle gevallen gecheckt is of die misschien ook een Mersenne-priemgetal opleveren.
Pure liefhebberij
Voor zover we nu kunnen overzien, heeft het zoeken naar zulke extreem grote priemgetallen geen nut. Het is pure liefhebberij. In de berichtgeving over de nieuwe recordhouder wordt soms gezegd dat grote priemgetallen nodig zijn voor het RSA-geheimschrift, dat onder meer het internetbankieren beveiligt.
Maar dat gebruikt priemgetallen van ‘maar’ een paar honderd cijfers; groot genoeg om RSA onkraakbaar te maken, maar klein genoeg om er snel mee te kunnen werken, zodat een internetbetaling geen uren hoeft te duren.

