Een virus zoals Ebola of HIV is moeilijk te bestrijden, omdat virussen veel sneller muteren dan planten of dieren. Dat maakt het lastig om hun DNA af te lezen. Wiskundige Jasmijn Baaijens ontwierp het eerste algoritme dat de genetische samenstelling van een onbekend virus ‘vanaf nul’ in kaart kan brengen.
Je kunt er op wachten: ergens op de wereld breekt een nieuwe, zeer besmettelijke en gevaarlijke virusziekte uit. Welk virus is het? Is het een nieuwe variant van Ebola of HIV? Of van het Zika-virus? Hoe snel muteert het? Waar is het ontstaan? Hoe wordt het overgedragen? Zijn er ook dragers zonder ziekte-symptomen? Wat zijn kansrijke aangrijpingspunten voor een vaccin of geneesmiddel?
Bij al deze vragen helpt het, als je de genetische samenstelling van het virus snel en volledig in kaart kunt brengen. Dat is bij een virus veel lastiger dan bij een dier- of plantensoort, omdat virussen veel sneller muteren. Vaak ontstaan in een patiënt tijdens het ziekteverloop al meerdere stammen van het virus.
Jasmijn Baaijens – inmiddels postdoc aan Harvard Medical School in Boston, maar in september gepromoveerd aan het Centrum voor Wiskunde en Informatica in Amsterdam – ontwikkelde diverse algoritmes om het DNA van virussen beter te kunnen analyseren. “Ik ben met dit onderzoek begonnen omdat dit type algoritmes me erg aansprak,” vertelt ze. “Bovendien was het erg actueel, er was toen namelijk een grote Ebola-uitbraak gaande in West-Afrika.”
Het DNA van een virus in kaart brengen bleek geen gemakkelijke klus. Het aflezen van het genoom (de volledige DNA-volgorde) van mens, dier of plant is daarmee vergeleken heel overzichtelijk: het DNA in alle cellen is hetzelfde, en de verschillen – mutaties – tussen individuen van één soort zijn relatief schaars. Ook is van de mens en veel dier- en plantensoorten al een referentie-genoom bekend, waar individuen maar weinig van afwijken.
In stukjes knippen
Het aflezen van een genoom kun je vergelijken met het leggen van een puzzel. Eerst moet je al het DNA met enzymen in kleine stukjes knippen. Die deels overlappende losse stukjes – de reads – zijn afleesbaar, maar daarna moet je de hele puzzel – met duizenden tot miljoenen stukjes – weer in elkaar zetten.
Het helpt enorm als er dan een referentie-genoom is. Dan zit er op het deksel van de doos met puzzelstukjes een voorbeeldplaat die hoogstens in details afwijkt. Zonder referentie-genoom heb je een doos met puzzelstukjes zonder voorbeeldplaat. Het leggen van zo’n puzzel noemt men het ‘de novo’ bepalen van een genoom.
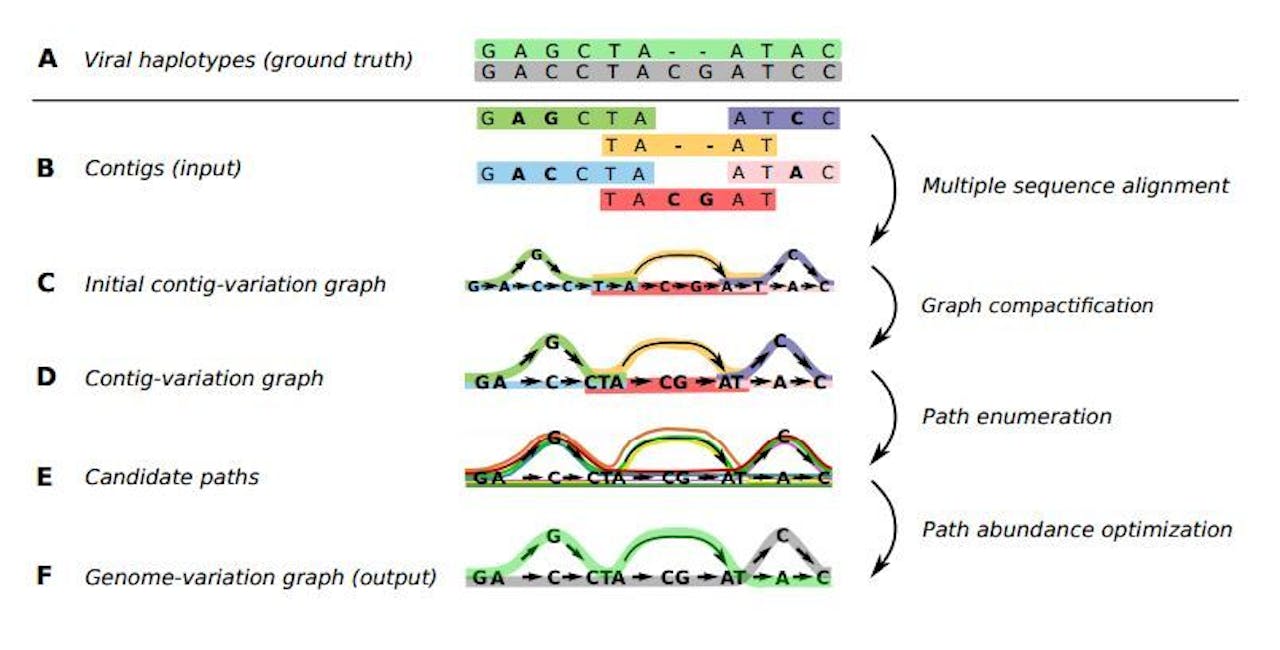
Schematisch beeld hoe de overlappende fragmenten DNA worden samengesteld tot diverse varianten van een virus-genoom.
Jasmijn BaaijensHet reconstrueren van een genoom uit de reads is eigenlijk een puur wiskundig probleem: je hebt een groot aantal fragmenten van ongeveer duizend letters lang (de genetische code gebruikt maar vier verschillende bouwstenen, gesymboliseerd door de letters C, G, A, T). Sommige van die fragmenten overlappen, omdat in de reageerbuis een groot aantal kopieën van het genoom geknipt wordt met enzymen – één DNA-molecuul is namelijk veel te klein om op deze manier te onderzoeken.
Door goed te kijken naar overlappende fragmenten, kun je achterhalen hoe het genoom is opgebouwd. Als de ene read bijvoorbeeld eindigt op ……. GTTAGCT, en een andere begint met AGCTAGC……, suggereert dit dat ze in het intacte genoom aan elkaar liggen, dus dat dit een fragment …….GTTAGCTAGC……. bevat.
Op deze manier kan een computer met een efficiënt zoekalgoritme alle, of zo veel mogelijk, reads aan elkaar puzzelen tot één geheel.
Spelfouten
Uiteraard is de praktijk weerbarstiger. Ten eerste maken alle sequencers (de machines die de DNA-fragmenten aflezen) soms fouten, zodat er ‘spelfouten’ in de reads zitten. Ook zou het kunnen, dat niet alle kopieën van het genoom exact hetzelfde zijn. Dit is zeker een mogelijkheid als je een bloedmonster analyseert van een patiënt waar duizenden virusdeeltjes in zitten die al tot verschillende stammen gemuteerd zijn. Stel, de computer reconstrueert twee lange fragmenten virus-DNA van tienduizend letters die identiek zijn, op vier letters na: is dat hetzelfde fragment met vier spelfouten, of horen beide fragmenten bij verschillende virus-stammen?
In haar proefschrift presenteert Baaijens diverse algoritmes die gebruik maken van grafentheorie om zulke vragen beter en sneller te beantwoorden dan tot nu toe mogelijk was. ‘Graaf’ is de wiskundige term voor een netwerk van knooppunten. Voor het aan elkaar puzzelen van de reads gebruikte Baaijens een zogeheten overlap-graaf (zie onderstaande afbeelding). Het idee om overlap-grafen te gebruiken is niet nieuw, maar was in onbruik geraakt omdat het voor grote genomen, zoals van de mens, té rekenintensief was om praktisch bruikbaar te zijn.
Voor het relatief kleine genoom van virussen kon ze deze methode echter wel geschikt maken, al moest ze toch nog nieuwe optimalisatietechnieken ontwikkelen om ervoor te zorgen dat de rekentijd binnen de perken bleef.
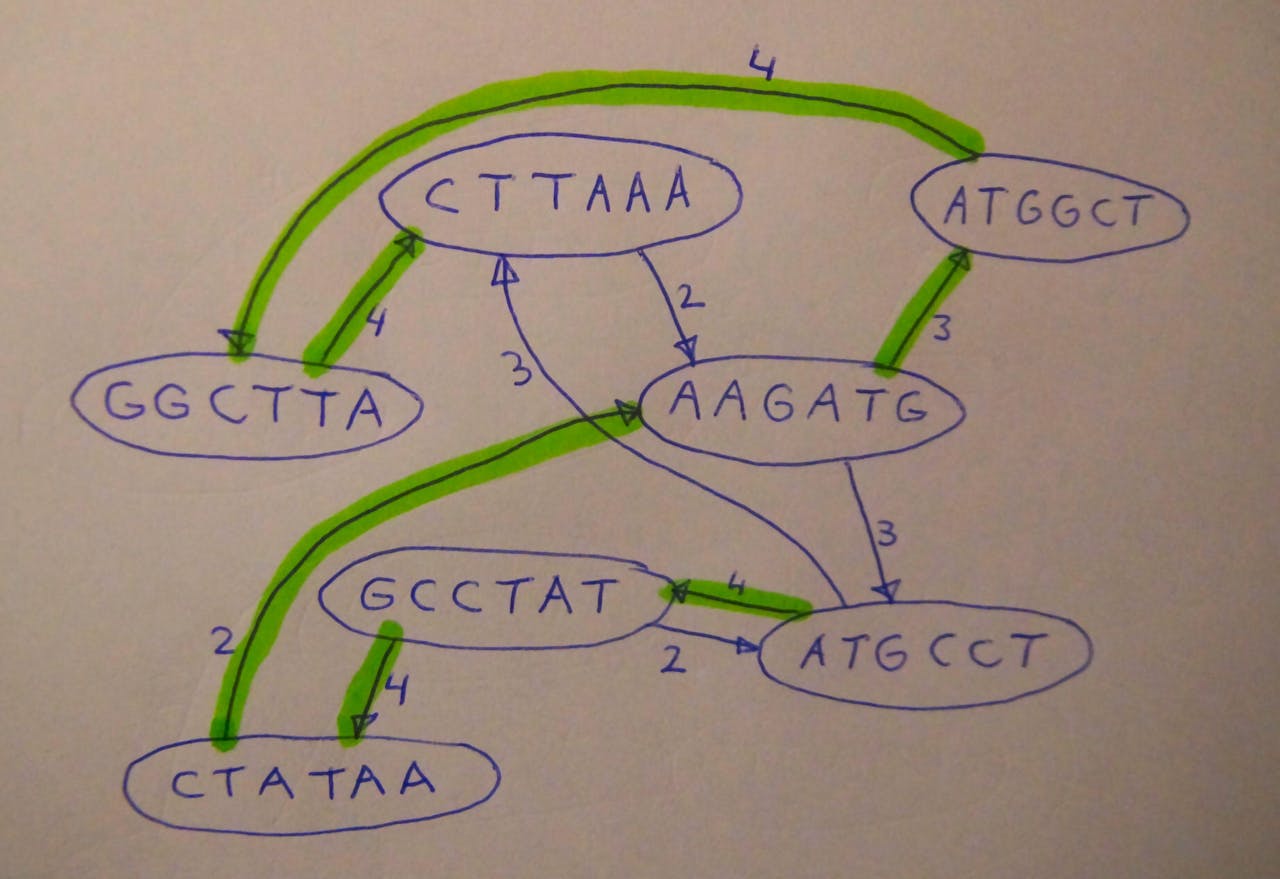
Principe van de overlapgraaf. Losse brokstukken (de knooppunten van de graaf) worden verbonden door een pijl als het eind van het ene brok minstens twee letters overlapt met het begin van een ander brok. Als je een volledige route langs alle knooppunten vindt, is er een goede kans dat dit het oorspronkelijke ‘genoom’ is, in dit geval ATGCCTATAAGATGGCTTAAA.
Arnout JaspersHet resultaat is een algoritme, SAVAGE (Strain Aware VirAl Genome assEmbler), waarmee het virale genoom in al zijn varianten met grote nauwkeurigheid bepaald kan worden, inclusief de percentages waarin elke variant voorkomt. Uiteraard is dit algoritme vervolgens getest op diverse sets bekende virale DNA-data, en de resultaten bleken significant beter dan die van al bestaande algoritmes op dit gebied.
Wetenschappelijk onderzoek eindigt maar al te vaak met voorlopige resultaten en als voornaamste conclusie dat verder onderzoek nodig is. Niet in dit geval. Baaijens stelt dat met dit proefschrift een serieus probleem in hoofdzaak gewoon opgelost is: het ‘de novo’ (letterlijk: vanaf nieuw, dus zonder voorkennis, ‘vanaf nul’) bepalen van een volledig virusgenoom met al zijn varianten.
YouTube-video over overlapgrafen
Niettemin, natuurlijk zijn nog verdere ontwikkelingen mogelijk. Stel bijvoorbeeld dat een genoom een herhaald fragment bevat dat langer is dan de reads. Dan krijg je een cykel (een gesloten ring van knooppunten) in de graaf. Immers, het pad dat het volledige genoom beschrijft, gaat twee keer langs hetzelfde knooppunt, namelijk die met het herhaalde fragment. Baaijens: “Dit is een erg lastig probleem dat op dit moment nog niet opgelost wordt door ons algoritme.”
Het nieuwe algoritme is ook toepasbaar om het genoom van snel muterende tumorcellen in een patiënt in kaart te brengen. In sommige gevallen kan dan de chemo- of immuuntherapie daar op afgestemd worden, zodat de tumor effectiever bestreden wordt.
Open source
Het is nu aan medisch onderzoekers om dit gereedschap aan hun arsenaal toe te voegen. Baaijens: “Ik denk dat de software in een stadium is waar het al wel door onderzoekers gebruikt kan worden, maar er zijn ook nog genoeg verbeterpunten. Ik hoop de software door te kunnen ontwikkelen zodat deze geschikt wordt voor algemeen gebruik. Tijdens mijn promotie-onderzoek heb ik zo nu en dan overleg gehad met virusonderzoekers die met name geïnteresseerd waren in HIV, om beter te begrijpen waar hun problemen en interesses liggen. De software is gratis te downloaden, ook de code is open source, dus iedereen kan die zelf aanpassen en doorontwikkelen.”
Zelf gaat ze nu in Boston werken aan het reconstrueren van het genoom van bacteriën: “Eigenlijk een vergelijkbaar probleem als dat van de virussen, maar op een hele andere schaal.” Bacteriën muteren namelijk ook snel, maar hun genoom is veel groter.

