Taxi’s staan een flink deel van hun tijd stil of rijden rond zonder passagier. Dat roept de vraag op hoeveel taxi’s minimaal nodig zijn om aan de vraag te voldoen. Voor dit ‘minimale-vlootprobleem’ is voor het eerst een wiskundige oplossing gevonden die ook praktisch bruikbaar is. Vooral zelfrijdende taxi’s kunnen daar baat bij hebben.
Hoe zet je vervoersmiddelen als vliegtuigen, bussen of taxi’s zo efficiënt mogelijk in? Daar is al uitgebreid onderzoek naar gedaan, want dit bespaart uiteraard kosten en voorkomt nodeloze uitstoot van broeikasgassen. Eerdere modellen om tot efficiënter taxivervoer te komen, gingen vaak uit van het delen van taxi’s door meerdere passagiers. Maar in de praktijk blijken mensen het vaak niet prettig te vinden om met een vreemde in de taxi te zitten, en zelden zal de taxi voor alle klanten de kortste route kunnen rijden.
Klantloze kilometers
Amerikaanse en Italiaanse onderzoekers hebben het nu over een heel andere boeg gegooid. Ze beschouwen de vraag naar ritten van individuele klanten als gegeven, en kijken hoe al die ritten met zo min mogelijk taxi’s uitgevoerd kunnen worden. Dat hangt natuurlijk ook af van hoeveel wachttijd voor de klant acceptabel is; immers, als een taxi er een uur over mag doen om een klant op te pikken, kan hij in z’n eentje twee klanten op grote onderlinge afstand van dienst zijn. Behalve de wachttijd voor de klant, heeft dit echter ook nog het nadeel dat die ene taxi veel klantloze kilometers maakt.
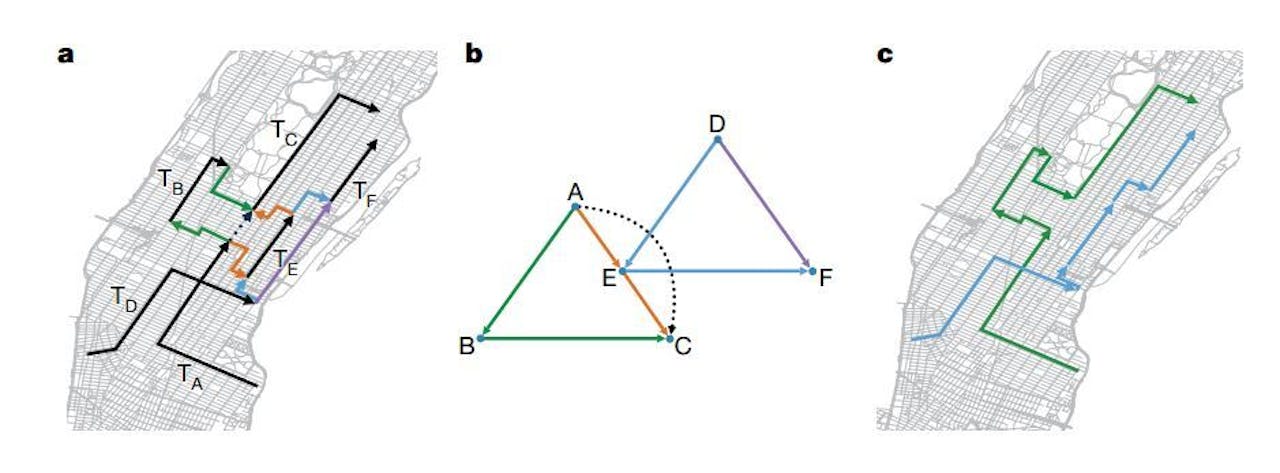
Een alternatieve manier om taxivervoer als netwerk weer te geven. a: zes taxiritten TA t/m TF in Manhattan. b: De ritten worden symbolisch weergegeven als punten A t/m F in een netwerk. Twee punten zijn verbonden als het mogelijk is (met een maximale wachttijd van 15 minuten voor de klant) dat dezelfde taxi beide ritten uitvoert. c: in dit geval is de optimale oplossing dat twee taxi’s de zes ritten uitvoeren volgens de aangegeven routes.
M. Vaziveh e.a., NatureDe randvoorwaarde was daarom dat klanten niet langer dan 15 minuten op een taxi hoefden te wachten. De onderzoekers berekenden vervolgens de optimale oplossing voor 150 miljoen taxiritten die in 2012 in New York plaatsvonden, waarvan de exacte tijd, plaats en duur bekend waren. In het echt waren die ritten uitgevoerd door (gemiddeld over het hele jaar) 7700 taxi’ s. Volgens de oplossing van het onderzoeksteam waren gemiddeld maar 4600 taxi’s nodig, wat een afname betekent van veertig procent. Tijdens de spitsuren reden in New York tien- à elfduizend taxi’s af en aan, terwijl er volgens de optimale inzet nooit meer dan zesduizend nodig zijn.
Toekomstige ritten
Helemaal reëel is die veertig procent reductie niet, omdat het algoritme dat de taxi’s toewijst beschikte over alle informatie over toekomstige ritten. In de werkelijke wereld moeten taxicentrales op basis van ervaringen uit het verleden en de drukte op het moment zelf beslissingen nemen over het inzetten van taxi’s.
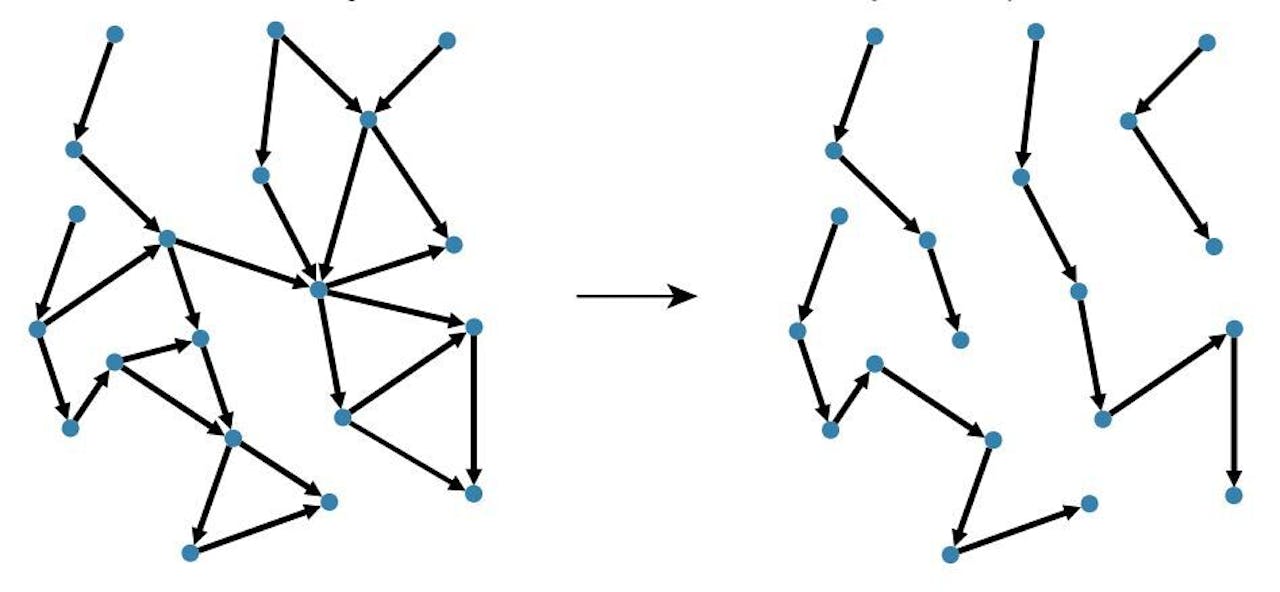
Het netwerk van taxiritten is wiskundig gesproken een ‘gerichte graaf’ (links). Het algoritme zoekt een manier om met zo min mogelijk paden alle knooppunten in de graaf af te gaan (rechts). Uiteraard moet elk pad daarbij aan voorwaarden voldoen die te maken hebben met de reistijd en de maximale wachttijd voor de klant, anders was één pad (taxi) altijd voldoende.
M.Vaziveh, NatureDaarom liet men het algoritme ook draaien in een variant waarbij het slechts keek naar welke aanvragen er in de afgelopen minuut waren binnengekomen, op grond waarvan het lokaal taxi’s toewees. Dan nog komt het systeem tot een oplossing waarin dertig procent minder taxi’s aan het werk zijn: gemiddeld genomen gaat het om negentig procent van de aangevraagde ritten binnen de maximale wachttijd van 15 minuten.
In vakblad Nature laten de onderzoekers zien dat het ‘minimale-vlootprobleem’ hanteerbaar wordt, als je elke rit beschouwt als een knooppunt in een netwerk, en elke verplaatsing (zonder passagier) tussen twee ritten als een verbinding tussen twee knooppunten. Deze aanpak is wezenlijk anders dan elke rit beschouwen als een verbinding tussen twee knooppunten (namelijk de plekken waar de klant in-, respectievelijk uitstapt).
In z’n algemeenheid beschouwd is dit type probleem NP-hard: dit wil zeggen dat er om principiële, wiskundige redenen geen algoritme bestaat, dat alle problemen van dit type in een redelijke rekentijd oplost. Maar dit taxiprobleem is een subcategorie waarvoor wel een
effectief algoritme bestaat, het Hopcroft-Karpalgoritme. Dit algoritme begint vrij willekeurig met een aantal korte paden door het netwerk, en puzzelt daar dan telkens nieuwe schakels aan, totdat het hele netwerk is opgedeeld. Volgens de onderzoekers kan dit algoritme zelfs voor tienduizenden taxiritten op een dag de optimale inzet snel genoeg kan berekenen om in de praktijk nuttig te zijn.
Menselijke eigenaardigheden
Dit onderzoek gaat wel uit van een centrale organisatie die alle taxi’s in een groot gebied aanstuurt. Dat is niet het geval in New York, waar een groot aantal aanbieders (waaronder veel freelance taxichauffeurs) aanwezig is. Ook hield het nog geen rekening met menselijke eigenaardigheden als de behoefte aan nachtrust of zoveel mogelijk willen verdienen.
Het model is daarom volgens de onderzoekers beter van toepassing op een centraal aangestuurde vloot van zelfrijdende taxi’s. Hoewel recente, geruchtmakende ongevallen met zelfrijdende auto’s twijfels wekken over de veiligheid, zien zij dit toch als de toekomst van het stadsvervoer.
Maar ook zelfrijdende auto’s zullen zichzelf regelmatig moeten opladen, en af en toe terug moeten naar de centrale voor een schoonmaakbeurt en onderhoud. Volgens de onderzoekers kunnen deze beperkingen, en die van menselijke chauffeurs, ook worden meegenomen in het algoritme: “Uitbreiding van het concept van het ‘vehicle-sharing’-network (…) moet nog verder worden onderzocht.”

