Een extreem hoge waterstand aan de kust die nu maar eens in de vijftig jaar voorkomt, zou in 2050 in de tropen elk jaar voor kunnen komen. Maar de gevaren die dit oplevert verschillen enorm per regio.
Het gevaar van zeespiegelstijging zit ‘m nauwelijks in de stijging van de gemiddelde waterstand. Overstromingen en dijkdoorbraken gebeuren vrijwel altijd op momenten dat alles tegenzit: als de waterstand door een stapeling van springtij, wind uit ongunstige richting en andere factoren extreem hoog is. De verwachte zeespiegelstijging tot halverwege deze eeuw – tien à twintig centimeter – is veel kleiner dan die vaak meters extra water door springvloed en golven tijdens een zware storm.
De kans op een extreme waterstand wordt meestal uitgedrukt in het aantal jaren dat gemiddeld tussen twee van die gebeurtenissen ligt. In een artikel in Scientific Reports hebben Amerikaanse onderzoekers nu voor alle kusten van de wereld uitgerekend wat de verwachte zeespiegelstijging tot 2050 doet met de frequentie van de lokale ‘eens in de vijftig jaar’-waterstand.

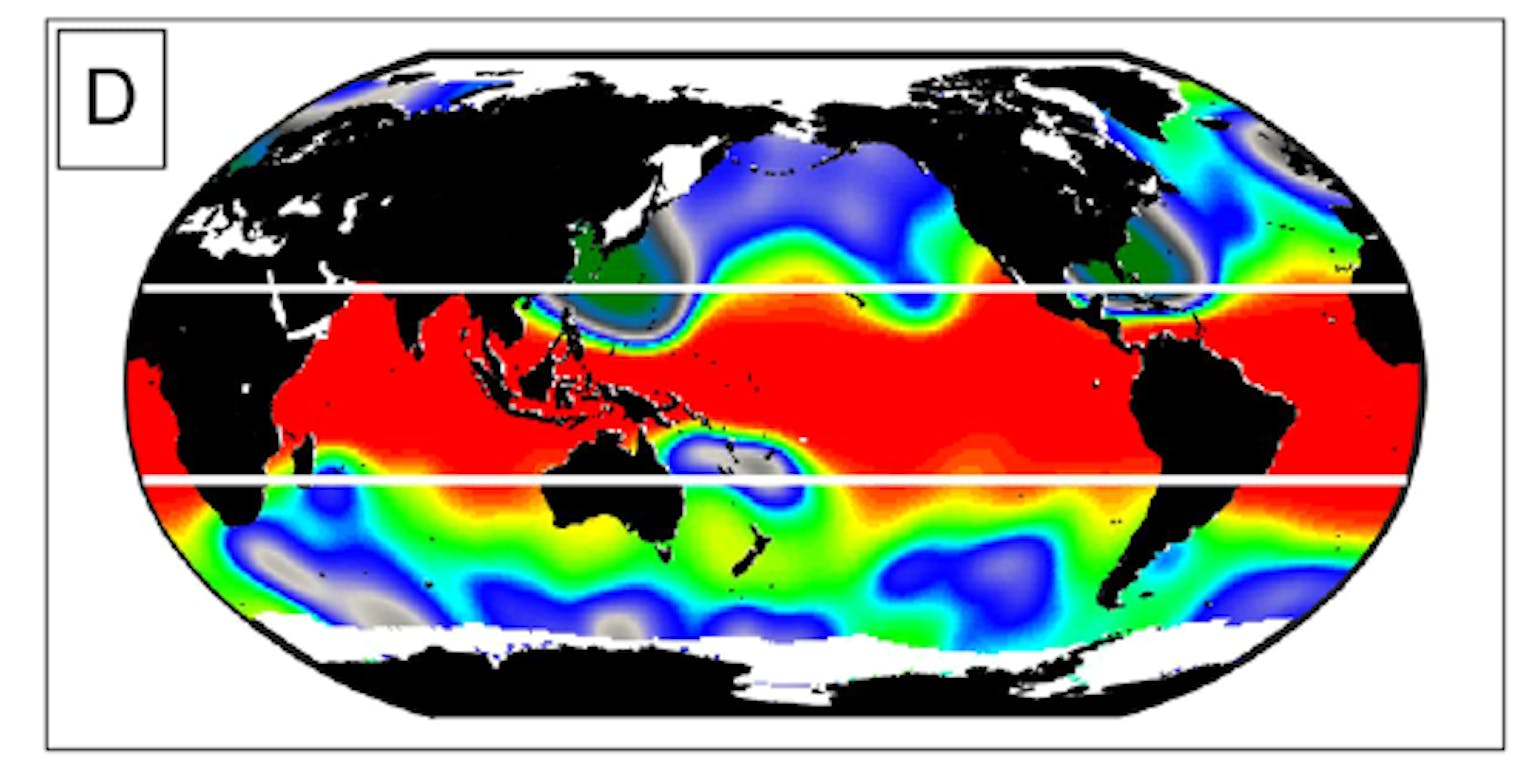
De zeespiegelstijging (in centimeters, zie kleurschaal rechts) waarbij extreme waterstanden die nu eens in de vijftig jaar optreden, eens in de vijfentwintig jaar voor zullen komen.
S. Vitousek, Nature Scientific ReportsTwee keer zo vaak
Aangezien de zeespiegelstijging veel kleiner is dan die andere, tijdelijke verhogingen van het waterpeil, zou je verwachten dat dit niet veel uitmaakt. Toch blijkt uit de berekeningen van Sean Vitousek en vijf collega’s dat die tien à twintig centimeter extra er op sommige kusten voor zorgt dat zulk extreem hoogwater veel vaker voorkomt: gemiddeld over de hele aarde twee keer zo vaak, maar met uitschieters tot meer dan honderd keer zo vaak. Dit paradoxale resultaat volgt uit de bijzondere statistiek van ‘extreme waarden’.
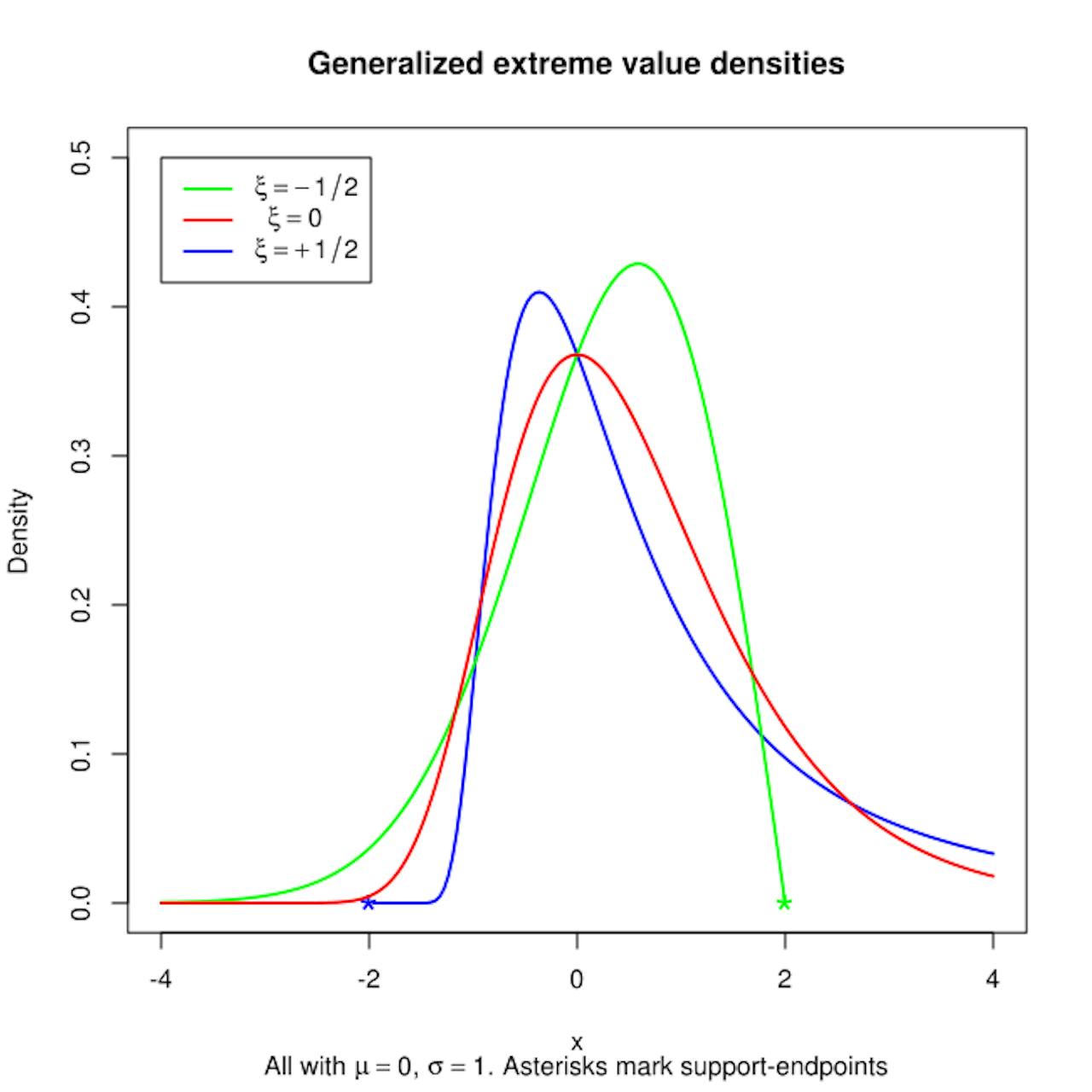
Deze statistiek gaat er van uit dat relatief grote uitschieters boven het gemiddelde vaker voorkomen dan je intuïtief zou verwachten. Ook neemt hun frequentie minder snel af met de grootte dan waar de ‘normale’ statistiek rekening mee houdt. Dit is de zogeheten ‘lange staart’ van de statistische verdeling van hoogwaterstanden (zie kader ‘Normale en extreme statistiek’ onderaan dit artikel).
Een fictief getallenvoorbeeld: stel dat bij de huidige zeespiegelhoogte, een waterstand van 3 meter boven een zeker vast merkteken (0 meter NAP) eens in de 50 jaar voorkomt, een stand van 2,9 meter eens in de 25 jaar, en een stand van 2,8 meter eens in de 10 jaar. Dan zal, mits alle overige omstandigheden gelijk blijven, al bij 10 centimeter zeespiegelstijging de oude ‘eens in de 50 jaar’-hoogte eens in de 25 jaar voorkomen – een verdubbeling van de frequentie. Bij 20 centimeter zeespiegelstijging zal de frequentie vervijfvoudigen. Dat beetje zeespiegelstijging is als het ware de druppel die de emmer veel vaker doet overlopen.
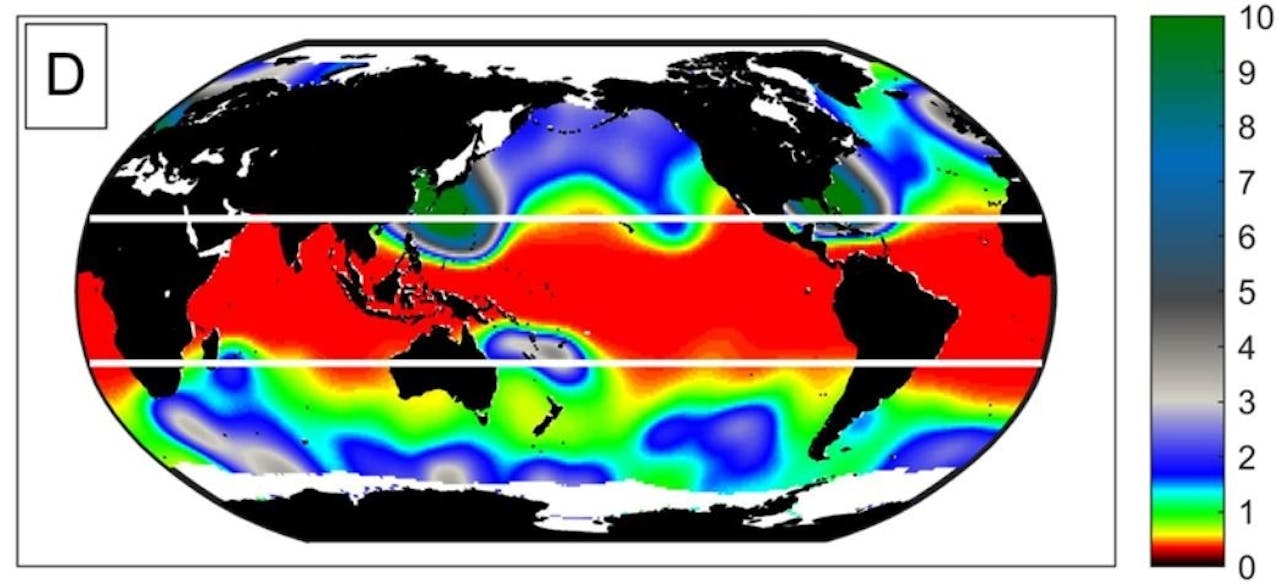
Bij een globale zeespiegelstijging van 25 centimeter – de meest pessimistische voorspelling voor 2050 – zal een extreme ‘eens in de vijftig jaar’-waterstand vaker optreden. De kleurcode rechts geeft, in jaren, aan hoe vaak. Dus aan een groot deel van de tropische kusten zal de ‘eens in de vijftig jaar’-waterstand gemiddeld elk jaar of nog vaker voorkomen.
S. Vitousek, Nature Scientific ReportsOverlopen
Maar wat is in dit geval ‘overlopen’? Het artikel in Scientific Reports en het persbericht spreken consequent van ‘overstroming’ (flooding). Sean Vitousek licht per e-mail toe: “Inderdaad gebruiken we ‘overstroming’ als algemene term, maar een overstroming is iets heel complex, het resultaat van een interactie tussen de waterhoogte, de vorm van de kust, de kustbescherming en de waterafvoer. Een vijftigjaarlijkse waterstand betekent nog geen vijfitgjaarlijkse overstroming, maar de waterhoogte is wel de meest populaire en simpelste indicator om te gebruiken. We hebben veel meer data over waterhoogtes dan over echte overstromingen.”
De grens van vijfitg jaar is gekozen, omdat deze in de VS gebruikelijk is voor het berekenen van dijkhoogtes en andere kustbescherming. In Nederland liggen de veiligheidsnormen veel hoger: wij bouwen dijken die pas falen bij een waterstand van eens in de vijfduizend of tienduizend jaar (berekend bij de huidige zeespiegel).
Welke invloed heeft twintig centimeter zeespiegelstijging op die frequentie? Volgens Vitousek is het effect van de ‘lange staart’ des te sterker naarmate je naar zeldzamere gebeurtenissen kijkt, dus zal die frequentie zelfs meer dan verdubbelen: “Die ‘eens in de vijfduizend jaar’ zou drastisch af kunnen nemen, tot misschien eens in de paar eeuwen, afhankelijk van het scenario voor de zeespiegelstijging. Niettemin zijn jullie dan nog steeds veel beter af dan wij (in de VS, red.), waar het vijftigjaarsniveau elke paar jaar overschreden zou kunnen worden.” De toename in frequentie geldt ook voor kleine, vaak voorkomende overstromingen, wat ze in de VS nuisance flooding (hinderlijke overstromingen) noemen.
Het effect van de zeespiegelstijging op de frequentie van hoogwater is in de tropen het sterkst, omdat de variatie door eb en vloed en stormen daar gemiddeld minder is dan verder van de evenaar af. Dus hetzelfde aantal centimeters zeespiegelstijging weegt rond de evenaar relatief het zwaarst. Daardoor kan op sommige tropische kusten de vijftigjaars-waterhoogte in 2050 zelfs ongeveer elk jaar gaan optreden.
Toch is dat minder dramatisch dan het misschien lijkt: als je dijken nu al bestand zijn tegen die ‘eens in de vijftig jaar’-waterstand, zijn ze daar ook tegen bestand als die elk jaar optreedt. De moraal van het verhaal is dus tweezijdig: als je niets doet, zullen toch al kwetsbare kusten veel vaker getroffen worden door overstromingen, maar een relatief kleine verhoging van de dijken is al genoeg om die frequentie weer drastisch terug te dringen. En lang niet alle kustgedeeltes zijn van nature kwetsbaar. Grote delen van de kust bestaan immers uit hoge rotsen of gebieden die toch al onbewoond zijn. Vitousek: “We zouden dit vraagstuk heel graag aanpakken met echte overstromingsdata, maar die zijn maar heel beperkt beschikbaar.”
Vitousek kent de Nederlandse waterbouwkundige prestaties uit eigen waarneming, en wil er graag nog iets over kwijt: “In m’n ruim twaalf jaar kustonderzoek heb ik enorm veel geleerd van Nederlandse onderzoekers en waterbouwkundigen. Volgens mij zijn de Nederlanders op dit gebied de beste ingenieurs ter wereld – ze moeten wel – en wat zij doen kan dienen als model voor de rest van de wereld om de kust weerbaarder te maken.”