Naar de content

De ongelooflijkste stelling van de wiskunde

Winnend profielwerkstuk over de Banach-Tarski-paradox

Joris de Man

Hoe kun je een massieve bol in een klein aantal stukken verdelen, om uit die stukken weer twee even grote massieve bollen samen te stellen? Scholier Joris de Man legt het uit in zijn profielwerkstuk. Dit heeft hij niet zelf ontdekt, maar hij legt wel een verrassend verband met virtuele deeltjes in de natuurkunde. Hij won de prijs voor het beste profielwerkstuk van het tijdschrift Pythagoras.

10 mei 2019

Het profielwerkstuk van Joris de Man heeft inmiddels ook de KNAW Onderwijsprijs gewonnen in de categorie Natuur & Techniek. Zijn werkstuk vind je hier.
De KNAW kiest elk jaar drie winnaars uit in elk van de vier profielen Natuur & Techniek, Natuur & Gezondheid, Economie & Maatschappij en Cultuur & Maatschappij. De overige prijswinnaars vind je hier

Een bol, of elke andere vorm die volume V heeft, kun je je voorstellen als een verzameling van een oneindig aantal punten die elk volume nul hebben. Wiskundig zeer slordig geformuleerd is dus
V= ‘oneindig x nul’.

Maar een oneindige verzameling kun je ook zodanig in tweeën delen dat beide helften nog net zo oneindig zijn. Bijvoorbeeld: je kunt de oneindige rij 0,1,2,3,4,5,…….. verdelen over de oneindige rijen 0,2,4,… en 1,3,5,… In zekere zin bevatten beide helften evenveel punten als het origineel. Stel nu dat je iets dergelijks kunt doen met de punten van die bol. Van beide helften maak je weer een bol. Als beide helften ‘evenveel’ punten bevatten als het origineel, hebben ze dan ook allebei hetzelfde volume V als het origineel?

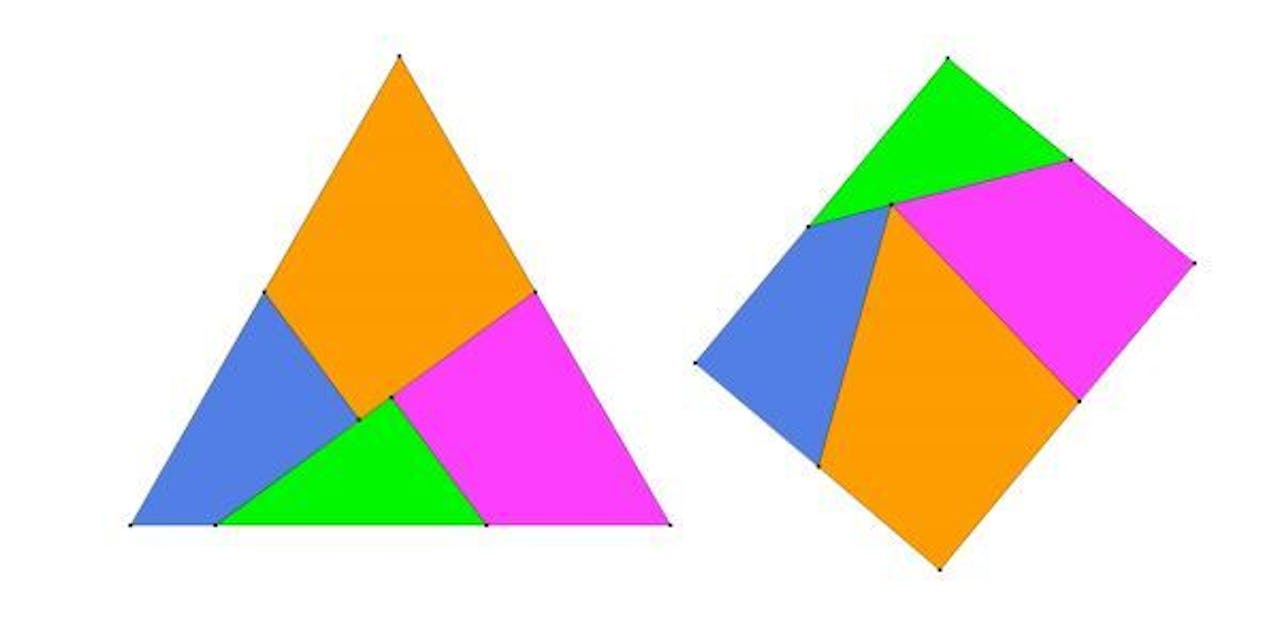
Voorbeeld van de gelijkverdeelbaarheid van twee verschillende vormen. Dit principe speelt een belangrijke rol in het bewijs van de Banach-Tarksi-paradox.

website Di-ss´e-quer

Het idee dat je uit een bol met volume V twee bollen met volume V kunt maken, klinkt volslagen absurd. Toch is dat wat de Banach-Tarski-paradox zegt.

Verdubbelen

De procedure is lang niet zo simpel als bij het ‘verdubbelen’ van de getallenrij. De belangrijkste reden is dat de getallenrij 0,1,2,3,4,… aftelbaar oneindig is: je kunt de getallen letterlijk tellen (zonder ooit te hoeven stoppen). Daarentegen bevat een volume in de driedimensionale ruimte overaftelbaar veel punten. Dit is een hogere graad van oneindigheid, omdat er geen procedure bestaat waarmee je al die punten systematisch kunt aftellen zonder tussenliggende punten over te slaan.

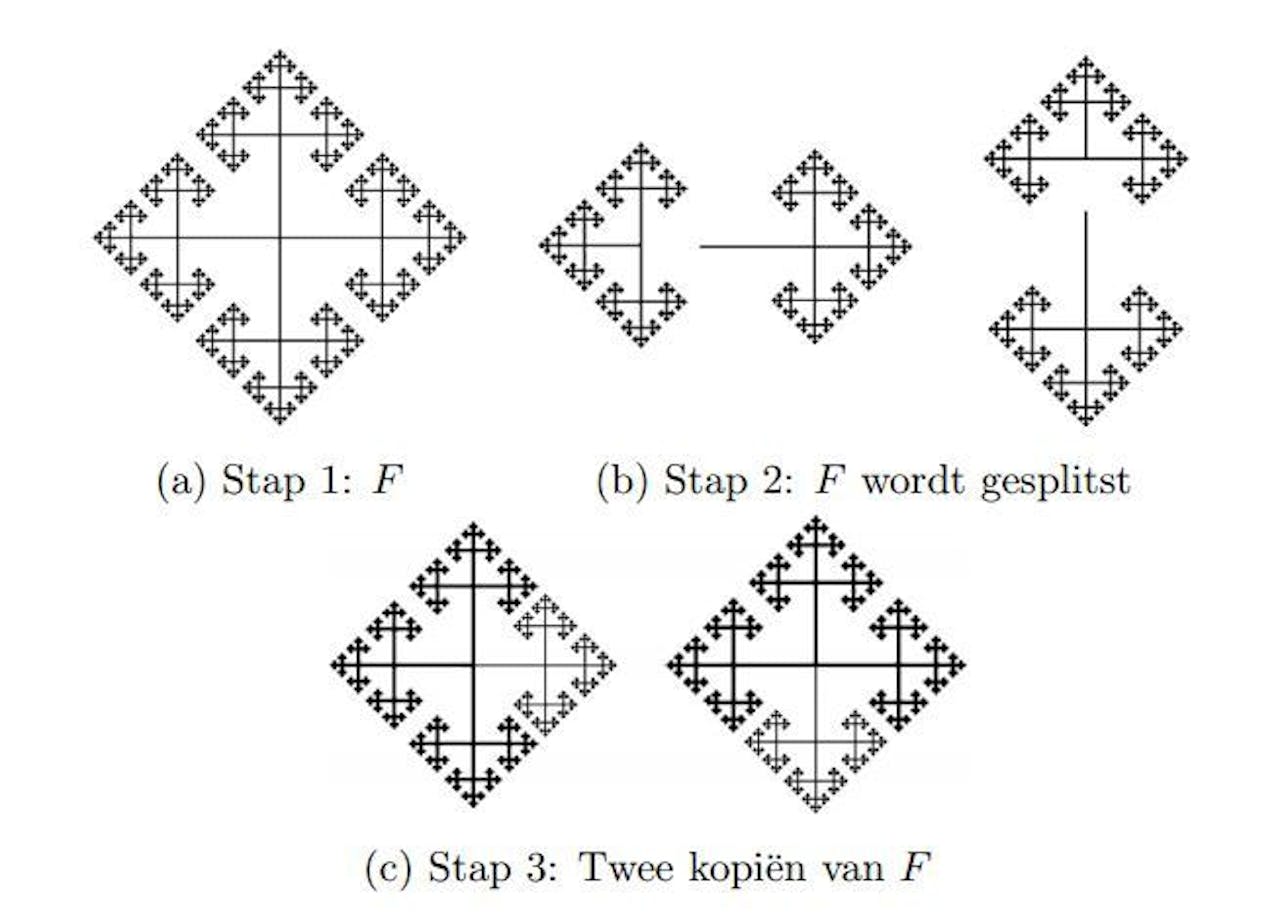
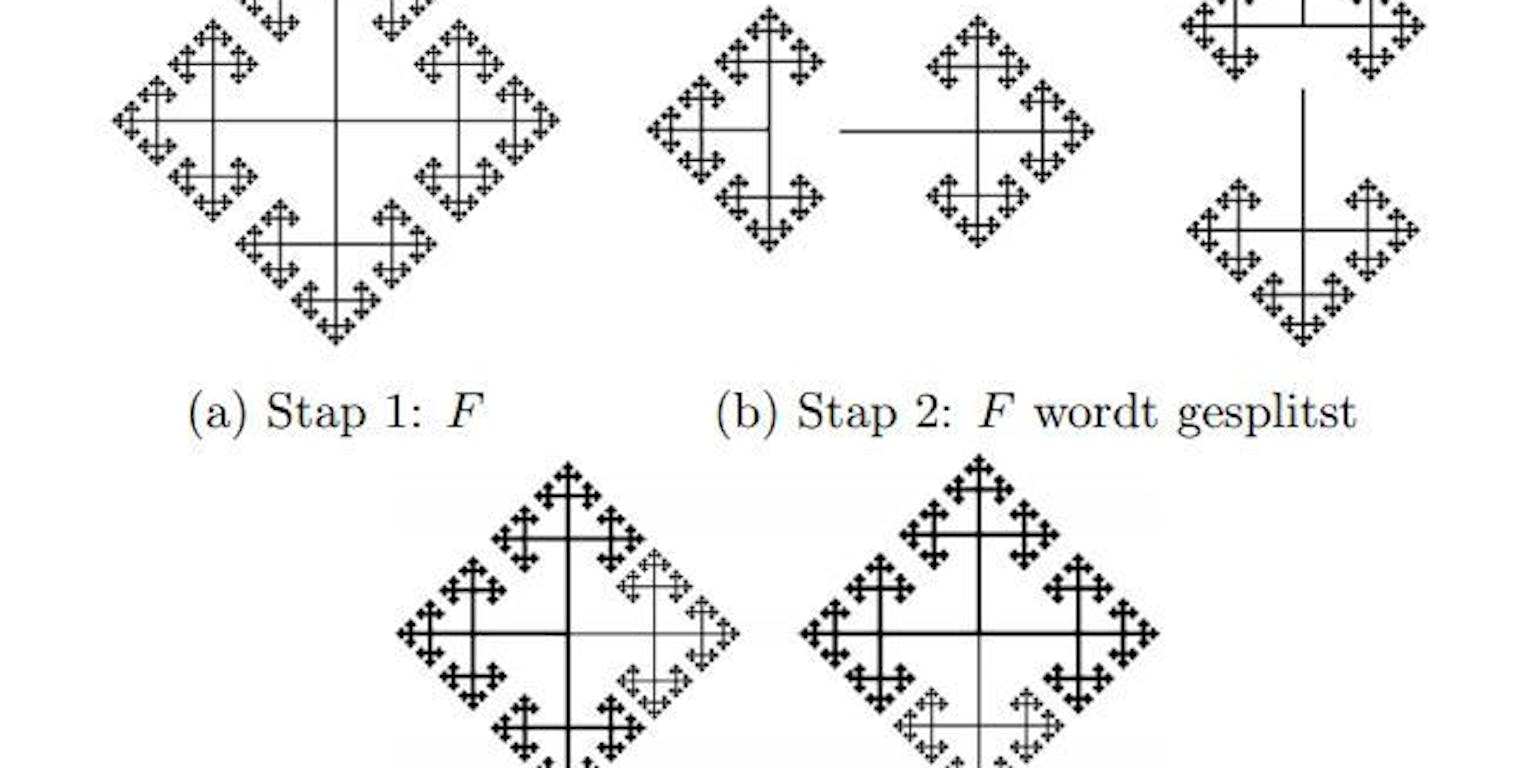
Deze fractal is een vorm met oneindig veel niveaus van vertakkingen. Door die op een slimme manier in vieren te splitsen, kun je er twee kopieën van het origineel van maken. De kopieën hebben niet minder (namelijk: ook oneindig veel) vertakkingen dan het origineel, zodat ze in wezen even groot zijn. Dit geeft een idee hoe een bol is op te splitsen in delen die samengevoegd de bol verdubbelen.

Joris de Man

Niettemin lieten Stefan Banach en Alfred Tarski in 1924 zien hoe je met een wiskundig strikt koosjere procedure een bol zodanig in stukken verdeelt, dat die samengevoegd twee even grote bollen opleveren. Later werd aangetoond dat de oorspronkelijke bol in minimaal vijf stukken verdeeld moet worden. Drie ervan vormen dan de ene bol, twee de andere bol.

Impressie van de delen waarin een bol kan worden opgesplitst om die te verdubbelen.

Rachel Levanger

Het bewijs van de Banach-Tarski-paradox stijgt ver uit boven de middelbare schoolwiskunde. Het is daarom een opmerkelijke prestatie dat Joris de Man met de benodigde geavanceerde concepten uit de verzamelingenleer en groepentheorie overweg kon. Bovendien verwerkte hij dat in een helder verhaal, dat laat zien dat hij deze lastige materie ook echt begrijpt.

Uit het juryrapport

“In twee fascinerende hoofdstukken wordt een uitstapje naar de natuurkunde gemaakt. Deze hoofdstukken zijn in grote mate speculatief. Het zou echter flauw zijn om de dwarsverbanden tussen natuurkunde en wiskunde die hij probeert te zien als verzinsels af te doen. Terecht citeert hij met Einstein: ‘Voorzover de stellingen van de wiskunde betrekking hebben op de werkelijkheid zijn ze niet zeker, en voorzover ze zeker zijn betrekken ze zich niet tot de werkelijkheid.’
Een van de grootste vragen uit de natuurkunde is: hoe goed past het wiskundige model op de werkelijkheid? Wat is werkelijkheid? En wat betekent passend? In een poëtisch laatste deel — De Conclusie — laat Joris de Man zich hier over uit.”

Voor een profielwerkstuk is dat al heel wat. Maar zoals het juryrapport ook constateert, waagt hij zich bovendien aan een bredere kijk op de Banach-Tarski-paradox. Als je die betrekt op alledaagse voorwerpen, zoals een volkoren bolletje, zijn de consequenties duidelijk absurd, zoiets als de wonderbare broodvermenigvuldiging door Jezus. Maar als je kijkt hoe deze paradox mogelijk in te passen valt in de moderne deeltjesfysica, wordt het een heel ander verhaal.

Deeltjes waarvan we vroeger dachten dat ze elementair waren, namelijk protonen, neutronen en mesonen, beschouwen fysici nu als opgebouwd uit quarks, die echter nooit afzonderlijk worden waargenomen. Protonen en neutronen bestaan elk uit drie quarks, mesonen uit twee quarks.
Verder spelen bij reacties tussen deze deeltjes virtuele deeltjes een cruciale rol, die slechts fracties van nanosecondes bestaan, en in die tijd allerlei natuurwetten, zoals de wet van behoud van energie, mogen schenden.

Virtuele deeltjes

Misschien, zo filosofeert De Man, is bij deze reacties tussen virtuele deeltjes sprake van Banach-Tarski-verdubbeling, waarbij de absurde consequenties op grotere schaal (zowel in ruimte als tijd) in toom worden gehouden door de wet van behoud van energie en andere natuurwetten. Op basis daarvan schetst hij een ingenieuze verklaring voor een al heel oud probleem in de natuurkunde: waarom er veel meer materie dan anti-materie in het heelal is.

Ook volgens De Man zelf is dit vooralsnog niet meer dan speculatie. Maar wel het soort speculatie waar anderen mee verder kunnen, en die aanleiding kan geven tot nieuw onderzoek of nieuwe theoretische inzichten. Of misschien doet hij dat ooit wel zelf.

De Pythagoras-prijs voor het beste wiskundige profielwerkstuk werd uitgereikt op het Nederlands Mathematisch Congres op 24 april 2019. Joris de Mans werkstuk, en die van de twee andere finalisten, zijn gepubliceerd op de website van het tijdschrift Pythagoras .

ReactiesReageer