Op de avond van 2 december 1966 stak L.E.J. Brouwer, gehuld in een paardendeken, zonder op of om te kijken de straat voor zijn huis over, en werd overreden. Daarmee kwam een plotseling eind aan het leven van Nederlands geniaalste en meest excentrieke wiskundige. Hij kende alle groten uit zijn tijd, zoals Einstein, Gödel, Wittgenstein en Hilbert. Hij bestreed dat ‘niet niet’ hetzelfde is als ‘wel’ en bewees dat het altijd ergens op aarde windstil is. 9 december eert een symposium zijn geestelijke erfenis.

Brouwer (midden) in 1923, met zijn collega’s Paul Urysohn (rechts) en Paul Alexandrov. Beide Pauls waren enthousiaste zwemmers, maar al een jaar later kwam Urysohn om bij een zwemongeluk aan de kust van Bretagne.
Koninklijke Bilbiotheek CC0Geen idylle
Luitzen Egbertus Jan Brouwer, in 1881 geboren in Overschie, onder de rook van Rotterdam, had geen idyllische herinneringen aan zijn geboorteplaats: “Het smerige vee dat op die weiden loopt, voedt zich met het afval van de jeneverstokerijen (…). Het dorp Overschie (…) wordt gekenmerkt door een smerige straat, een lelijk stadhuis, lelijke particuliere huizen, enkele mesthopen, en een ophaalbrug in het midden.”
Dit schreef hij op zijn zestiende in een mini-autobiografie. Naar school is hij niet veel geweest, meestal werd hij thuis door zijn ouders onderwezen. Daarna volgde een studie wiskunde aan de Universiteit van Amsterdam. Hij noch zijn ouders koesterden enige twijfel aan zijn genialiteit: “Nog enige jaren zal ik obscuur moeten zijn, dan zal mijn greep gevoeld worden”,schreef hij op z’n drieëntwintigste in zijn dagboek. En dat kwam binnen tien jaar nog uit ook.

Een van Brouwers beroemdste ontdekkingen is de dekpuntstelling. Vrij vertaald zegt die, dat hoe lang je ook roert in een kopje koffie of een blik verf, er altijd een punt van de vloeistof is – het dekpunt – dat zich weer op precies dezelfde plek bevindt als aan het begin. Zolang je roert, is dit telkens een ander punt, maar altijd is er minstens één waarvoor dit geldt.
Ironisch is, dat deze stelling niet voldoet aan Brouwers eigen intuïtionistische principes. De dekpuntstelling zegt namelijk dat zo’n punt bestaat, maar niet waar het te vinden is.
Intuïtionistische bewijzen moeten ‘constructief’ zijn: het bewijs voor de dekpuntstelling zou ook een recept moeten geven om het dekpunt te vinden. Later heeft Brouwer een variant van de dekpuntstelling wel volgens intuïtionistische principes bewezen.
Rubbermeetkunde
Toen had hij een paar baanbrekende stellingen bewezen in de topologie, de tak van wiskunde die zich bezighoudt met de eigenschappen van objecten in een ruimte van twee, drie of meer dimensies, ongeacht hoe je ze vervormt. Daarom noemt men de topologie ook wel rubbermeetkunde. Voor een topoloog is een cirkel hetzelfde als een vierkant, want je kunt de één elastisch vervormen tot de ander. Hetzelfde geldt voor een donut (torus) en een koffiekopje (die hebben allebei één gat), of een bol en een kubus (geen gaten). Maar zonder knippen kun je van een bol geen torus maken.
Rond 1910 ontdekte Brouwer zijn fameuze dekpuntstelling (zie afbeelding Onvolmaakt roeren), die tot de paradoxale conclusie leidt, dat je met roeren in een kopje nooit alle vloeistof tegelijk van zijn plaats krijgt. Kort daarna bewees hij een algemene eigenschap van stromingspatronen op boloppervlakken, die onder meer impliceert, dat het altijd ergens op aarde perfect windstil moet zijn! (zie afbeelding Volmaakte windstilte)
Maar toen zijn reputatie ook internationaal gevestigd was, ging hij zich steeds meer wijden aan onderzoek dat de grondslagen van de wiskunde in twijfel trok. Hij formuleerde eigen principes om wiskunde te bedrijven, het intuïtionisme. Dat was in de jaren twintig en dertig van de vorige eeuw.
De niet uitgesloten derde
Brouwer richtte zijn pijlen met name op de ‘wet van de uitgesloten derde’. Die houdt in, dat iets óf waar is, óf niet waar, een derde mogelijkheid is er niet. Brouwer zelf gaf als voorbeeld de bewering: ergens in de oneindige rij decimalen van het getal pie (3,141572…..) komt een serie van 99 cijfers 9 voor.
Waarschijnlijk moeten we ongeveer 1099 decimalen van pie uitrekenen voordat we zo’n serie tegenkomen – als die voorkomt – maar dat zal nooit gebeuren. Immers, 1099 – een 1 met 99 nullen – is groter dan het aantal atomen in het zichtbare heelal, vermenigvuldigd met het aantal seconden sinds de oerknal.
Zolang we geen methode hebben om deze bewering te checken, mag je volgens Brouwer niet zeggen dat deze óf waar, óf onwaar is. Dat getuigde van een vooruitziende blik: later bewees Kurt Gödel met zijn fameuze onvolledigheidsstelling, dat sommige wiskundige beweringen principieel onbeslisbaar zijn.
Wat is nu de status van Brouwers grondslagenstrijd? Leeft het intuïtionisme nog? Wim Veldman, wiskundige aan de Radboud Universiteit: “In sommige opzichten wel.” 9 december wordt in Amsterdam een internationaal symposium over Brouwers werk gehouden. Veldman kijkt vooral uit naar de bijdragen van Michael Rathjen en van Yannis en Joan Moschokavis over verzamelingenleer, en die van de befaamde Amerikaanse filosoof Saul Kripke.
Duister
Het symposium is bedoeld voor specialisten. Zelfs veel wiskundigen vinden Brouwers intuïtionisme duister, of hebben de neiging het af te doen als moeilijk doen over niks. Ten onrechte, volgens Veldman: “Brouwer verdient het om wel serieus genomen te worden. De klassieke wiskunde past bij het redeneren over wiskundige objecten de logica van eindige aantallen objecten ten onrechte toe op oneindige aantallen.”
Brouwers intuïtionisme was een reactie op het heersende optimisme onder wiskundigen in de jaren twintig. Uit een paar onbetwijfelbare basiswaarheden, de axioma’s, zou met absolute zekerheid elke wiskundige waarheid af te leiden zijn. Wiskunde was zoiets als schaken, en de waarheid bestond uit elke schaakstelling die je met legitieme zetten vanuit de beginstand kon bereiken. De kampioen van deze ‘axiomatische’ opvatting was de Duitser David Hilbert, die zijn instituut in Göttingen tot het centrum van de wiskundige wereld gemaakt had.
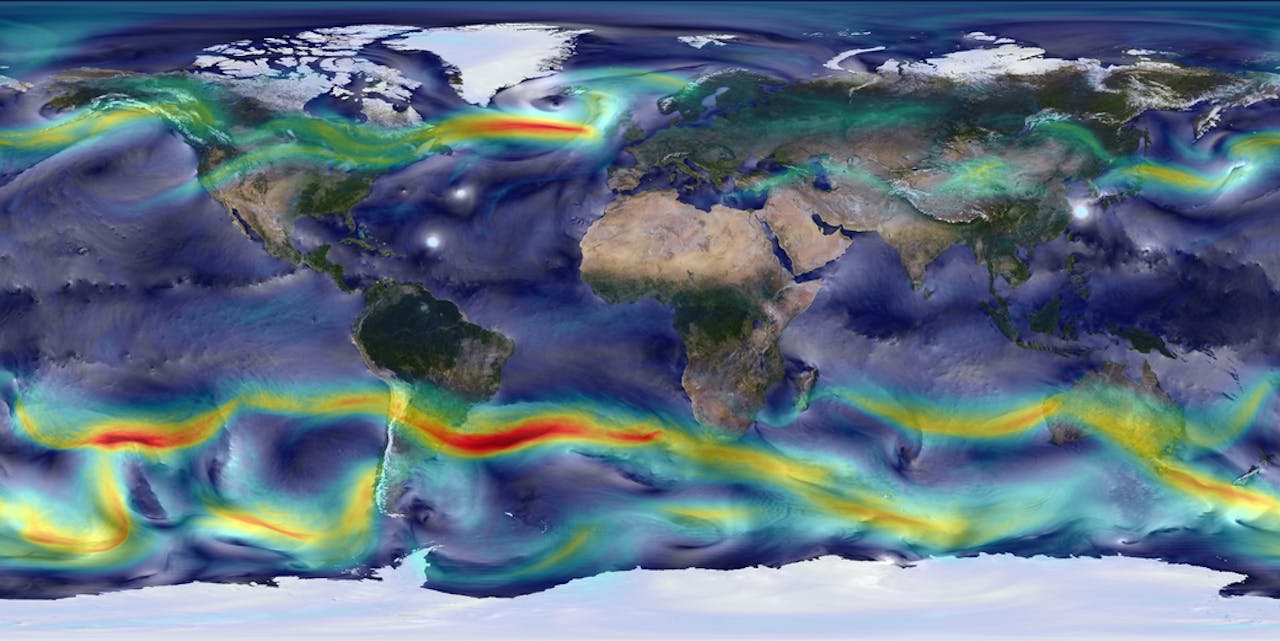
Volmaakte windstilte
Een andere door Brouwer bewezen stelling impliceert dat het altijd ergens op aarde volmaakt windstil is. Als je de windsterkte en -richting in elk punt van het aardoppervlak voorstelt door een pijltje (wiskundigen zeggen: vector) kun je op een bol namelijk geen pijltjespatroon (vectorveld) tekenen, zonder dat ergens een punt ontstaat waar alle pijltjes naar elkaar toe of van elkaar af wijzen. In dat punt is het windstil. Een andere manier om dit te illustreren is: wanneer je een behaarde bol probeert te kammen, is er altijd een kruintje.
Brouwer bestreed de geldigheid van dit ‘bewijs uit het ongerijmde’ als het over oneindige verzamelingen van wiskundige objecten gaat. En dat is al snel het geval: elke eigenschap van de natuurlijke getallen (1,2,3,4,……) die je bewijst, gaat over oneindig veel getallen. Ook Hilberts stellingen gingen over de oneindige verzameling van alle mogelijke krommen (‘kromme’ is de naam voor elke mogelijke formule die je kunt weergeven als een lijn in een grafiek). Brouwer viel de wet van de uitgesloten derde al in 1908 aan, toen hij nog onbekend was, maar pas na zijn topologische prestaties begon dit standpunt de aandacht te trekken.
Hilbers ontdekkingen zijn te gecompliceerd om hier uiteen te zetten, maar een veel simpeler, klassiek voorbeeld hoe je iets bewijst over oneindige verzamelingen, is het diagonaalargument van Georg Cantor (zie kader Diagonaal denken). Daarmee toonde hij aan, dat er verschillende graden van oneindigheid bestaan. Zo is ‘aftelbaar oneindig’ een lagere graad van oneindigheid dan ‘overaftelbaar oneindig’. Tot die laatste categorie behoren de reële getallen, dus alle getallen met (eventueel oneindig veel) decimalen achter de komma.
Veldman: “De kwestie die Brouwer obsedeerde was: hoe moeten we denken en zinvol spreken over een overaftelbare verzameling, zoals de verzameling van de reële getallen.” In Brouwers intuïtionistische opvatting van de wiskunde moet een existentiebewijs constructief zijn: het moet een recept bevatten om het ding waarvan je het bestaan wilt bewijzen, ook echt te vinden. Veldman: “Het diagonaal-argument is helemaal constructief, daar had Brouwer geen moeite mee.” Immers, Cantor geeft een recept om het getal te vinden dat je nodig hebt om het bewijs rond te maken. Hilberts stellingen doen dat niet, die bewijzen slechts dat een bepaald object ‘niet-niet’ bestaat.
Constructief
Het intuïtionisme van Brouwer is veeleisend: allerlei algemeen geaccepteerde bewijzen in de wiskunde zijn zonder de wet van de uitgesloten derde niet meer geldig. Die moeten ‘constructief’ over gedaan worden, wat doorgaans veel moeilijker is.
Veldman: “Stellingen uit de gangbare wiskunde kunnen op verschillende manieren intuītionistisch precies geformuleerd worden. Sommige versies kunnen waar blijken, andere versies onwaar, of er kan een versie tevoorschijn komen waarvan we niet weten of hij waar is of niet.” Vandaar dat er nog altijd wiskundigen zijn, die Brouwers intuïtionistische onderzoek voortzetten.
Hoewel Brouwer en Hilbert in de jaren twintig groot respect voor elkaars prestaties hadden, raakte de verhouding tussen de twee later ernstig verzuurd door Brouwers compromisloze intuïtionisme. Toen Hilbert hem in 1928 uit de redactie van het tijdschrift Mathematische Annalen zette (destijds de absolute wereldtop om in te publiceren), raakte Brouwer verbitterd en geïsoleerd. Ook zijn wiskundige productiviteit nam sterk af, zoals zo vaak bij oudere wiskundigen.
Mythevorming
Brouwer was een extreem eigenzinnig mens, over wie veel anekdotes en mythes de ronde deden. Meestal woonde hij in een vakantiehutje op een eigen stuk grond in Blaricum, met een coterie van vrouwelijke bewonderaars om zich heen. Daar liep hij soms spiernaakt rond, waar zijn metgezellen niet van op of om keken.
Naast de wiskunde, stak hij heel wat energie in de Signifische Kring, een genootschap van filosofen en schrijvers, waaronder Frederik van Eeden, dat beoogde de maatschappij totaal te hervormen. Dat ze met hun excentrieke taal- en levensfilosofie geen enkele weerklank vonden, noch bij de elite, noch bij het volk, schenen ze nauwelijks op te merken.
Brouwer was behalve streng wiskundige ook mysticus, wat hij niet als een tegenstelling zag. In zijn jonge jaren heeft haar daar zelfs een serie openbare lezingen over gegeven. Dit en nog veel meer is al in 2002 opgetekend door wiskundige Dirk van Dalen, in diens fascinerende biografie L.E.J. Brouwer, Het heldere licht van de wiskunde (daaruit komen ook de citaten van Brouwer in dit artikel).
Brouwers mystieke overtuigingen en zeker een deel van zijn maatschappijkritiek mogen we inmiddels wel achterhaald noemen. Hoe zit dat met zijn wiskunde? Veldman is er van overtuigd dat die nog steeds relevant is. Ook voor wiskundigen die geen specialist zijn in het intuïtionisme is die waardevol: “Je leert er grotere precisie van, ook als je je daarna geen zorgen meer maakt over die grondslagen. De kritiek van Brouwer is iets wat alle wiskundigen zich aan moeten trekken.”

