Vrijwel niemand jonger dan veertig kan nog een beetje behoorlijk hoofdrekenen. Maar hoofdrekenen als topsport speelt zich af op een heel ander niveau, waar praktisch nut er niet toe doet. Willem Bouman, een van de beste hoofdrekenaars ter wereld, doet er in zijn boek niet geheimzinnig over: het is een kwestie van veel uit het hoofd leren en heel veel oefenen.
Een kijksport zal het niet snel worden, maar in hoofdrekenen worden jaarlijks wereldkampioenschappen gehouden. De deelnemers moeten reeksen getallen van tien cijfers bij elkaar optellen, uit getallen van zes cijfers de wortel trekken tot vijf cijfers achter de komma, en andere taken die voor een rekenmachientje van een paar euro geen enkel probleem zijn.
Een rekenwonder als Wim Klein (1912-1986) had, toen computers of rekenmachientjes nog geen gemeengoed waren, een echte baan als rekenaar bij onderzoeksinstituut CERN, maar hij trad ook op als variétéartiest met zijn rekenkunst, vaak onder de naam Willie Wortel. Tegenwoordig valt met hoofdrekenen geen droog brood meer te verdienen, en wordt dit genre nog slechts beoefend door een zeer select groepje ware liefhebbers. Willem Bouman is een van hen, die nu zijn vaardigheden uit de doeken doet in het boek De kunst van het hoofdrekenen.
Tiencijferige getallen
Om een recensie-exemplaar van het boek toegestuurd te krijgen, gaf ik telefonisch aan de auteur m’n adres door, met postcode natuurlijk. “Aha, twee kwadraat maal drie maal honderddrieennegentig”, antwoordde deze onmiddellijk. Willem Bouman geldt als een van de beste hoofdrekenaars ter wereld. In het Duitse tv-programma Superhirn, in september 2016, slaagde hij erin om uit het hoofd twee tiencijferige getallen a en b te berekenen waarvan alleen de som a+b (tien cijfers) en het product a x b (twintig cijfers) gegeven waren.
Algebraïsch is dit een simpel probleem: twee vergelijkingen, twee onbekenden, je kunt a en b altijd vinden door het oplossen van een kwadratische vergelijking. Maar dat houdt wel in, dat je uit het hoofd onder andere een getal van tien cijfers moet kwadrateren, en een wortel moet trekken uit een getal van twintig cijfers. Echter, een hoofdrekenaar is niet op zoek naar een algemene oplossingsmethode van een probleem, hij is op zoek naar een concrete uitkomst. Een groot deel van het ambacht bestaat dan ook uit allerlei handigheidjes en technieken die in sommige gevallen snel de juiste uitkomst geven.
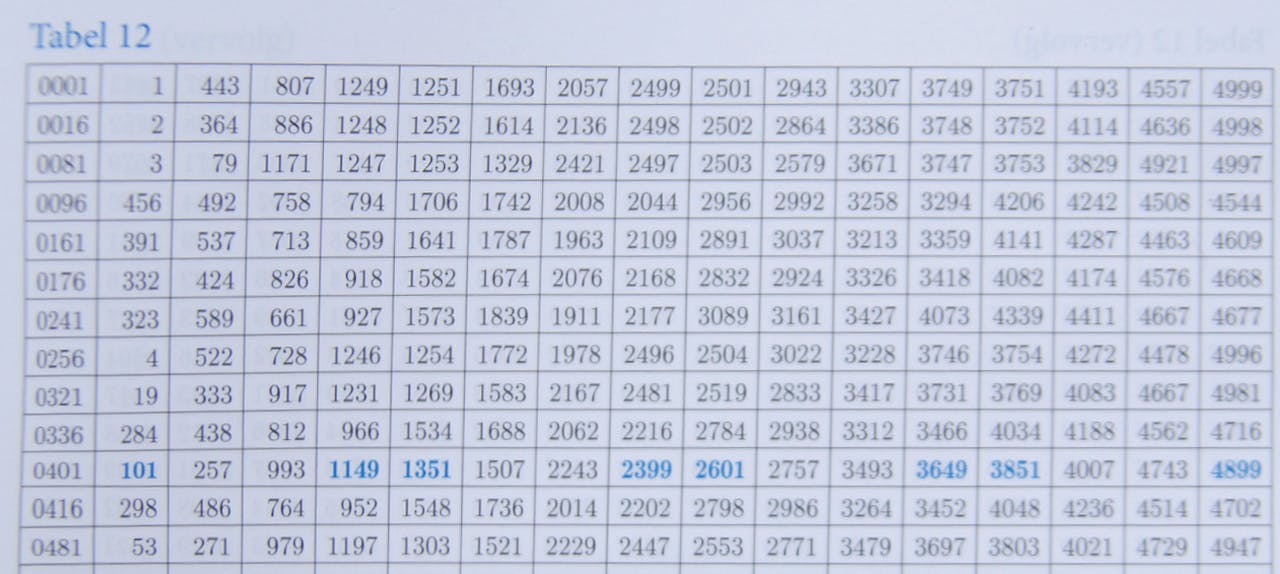
Het begin van een tabel die de vierdemachten van alle gehele getallen tot 10.000 rangschikt op de vier eindcijfers (de kolom uiterst links). Hoofdrekenaars leren delen van zulke tabellen uit het hoofd, en zoeken naar systematiek in de getallen waardoor ze er nog meer beschikbaar hebben voor berekeningen met grote getallen.
W.BoumanSuperbrein
Zo heeft hij nog veel meer tabellen en trucs in zijn mentale gereedschapskist om dit soort schijnbaar onmogelijke berekeningen zonder hulpmiddelen aan te pakken. Bouman laat in zijn boek ook zien dat niet alle ‘bovenmenselijke’ rekenprestaties echt bijzonder zijn. Zo is het trekken van een dertiende- of negentiendemachtswortel uit een getal van honderd cijfers verrassend simpel. Althans, als je lange tabellen met logaritmes en machten van de getallen onder de honderd uit je hoofd kent. Maar dat spreekt op dit niveau vanzelf.
Talent
In zijn boek geeft Bouman een nuchter overzicht van de kunst van het hoofdrekenen (persoonlijk zou ik het eerder een ambacht noemen), die vooral gebaseerd is op veel oefenen en veel uit het hoofd leren. Talent als rekenwonder zit misschien meer in het doorzettingsvermogen om het te willen worden dan in een mysterieus, aangeboren rekenvermogen.
Bouman en andere hoofdrekenaars hebben wel contacten met wiskundigen, maar bekommeren zich niet om wiskundige bewijzen of abstracte eigenschappen van getallen. Wat niet wegneemt dat creativiteit een rol speelt: elke hoofdrekenaar vult zijn gereedschapskist op zijn eigen manier. Zo maakt Bouman veel gebruik van modulo-rekenen. Modulo-10 rekenen kent iedereen: dat komt neer op alleen maar rekening houden met het laatste cijfer van een getal. Maar Bouman gebruikt ook rekenen modulo-41 en modulo-101 om snel bewerkingen op grote getallen uit te voeren.
Het boek is een prima handleiding voor wie zich in het hogere hoofdrekenen wil verdiepen. De auteur vult dit aan met anekdotes uit zijn leven die ons iets zouden moeten vertellen over de waarde van hoofdrekenen in het dagelijks leven, maar die wat mopperige intermezzo’s voegen weinig aan het boek toe.

