Inmiddels lijkt heel Nederland aan het rekenen te zijn aan het nieuwe coronavirus. Als individu kan je honderden besmettingen voorkomen, laten de simpelste sommetjes zien. Maar of we genoeg IC-bedden hebben kunnen zelfs de meest geavanceerde modellen ons niet vertellen. Welke rekenmethoden zijn er in omloop en wat heb je er aan?
Sinds een week of twee lijkt Nederland geen zeventien miljoen bondscoaches meer te tellen, maar zeventien miljoen epidemiologen. Niet gehinderd door enige kennis van zaken kruipen we achter onze rekenmachines, en verkondigen op Facebook en Twitter hoeveel ziekenhuisopnamen en sterfgevallen de coronacrisis ons nog op gaan leveren.
Sommige van die sommetjes zijn best zinvol. Niet vanwege hun voorspellende waarde, wel om te begrijpen hoeveel verschil je als individu kan maken – gewoon door thuis te blijven en de 1,5 meter afstand in acht te nemen.
Maar hoe zit het eigenlijk met de modellen die de echte epidemiologen maken? Hoe rekent het RIVM de mogelijke scenario’s door? NEMO Kennislink duikt in de getallen, en loopt zowel de bierviltjesberekeningen als de geavanceerde modellen voor u langs.

Exponentiële groei
De vervelendste eigenschap van de snelheid waarmee een virus zich verspreidt, is dat dit exponentieel gebeurt. Dit betekent dat het aantal besmettingen per dag niet steeds met grofweg hetzelfde aantal toeneemt, maar met grofweg dezelfde factor. Dit veroorzaakt explosieve groei – zoals we dat ook kennen van guppies, konijnen, en de paar luizen op het hoofd van je kind die na een dag of drie opeens met zijn honderden blijken te zijn.
Het RIVM gaat ervan uit dat één drager van het virus in Nederland – als er geen maatregelen van kracht zijn – gemiddeld ongeveer twee anderen besmet. Dit betekent dat het aantal nieuwe virusdragers per overdracht verdubbelt: bij de eerste overdracht van één naar twee, bij de tweede overdracht van twee naar vier, bij de derde overdracht van vier naar acht. Na de tiende overdracht zit je dan 1024 nieuwe gevallen, en bij de vierentwintigste keer overspringen besmet het virus 17 miljoen nieuwe mensen.
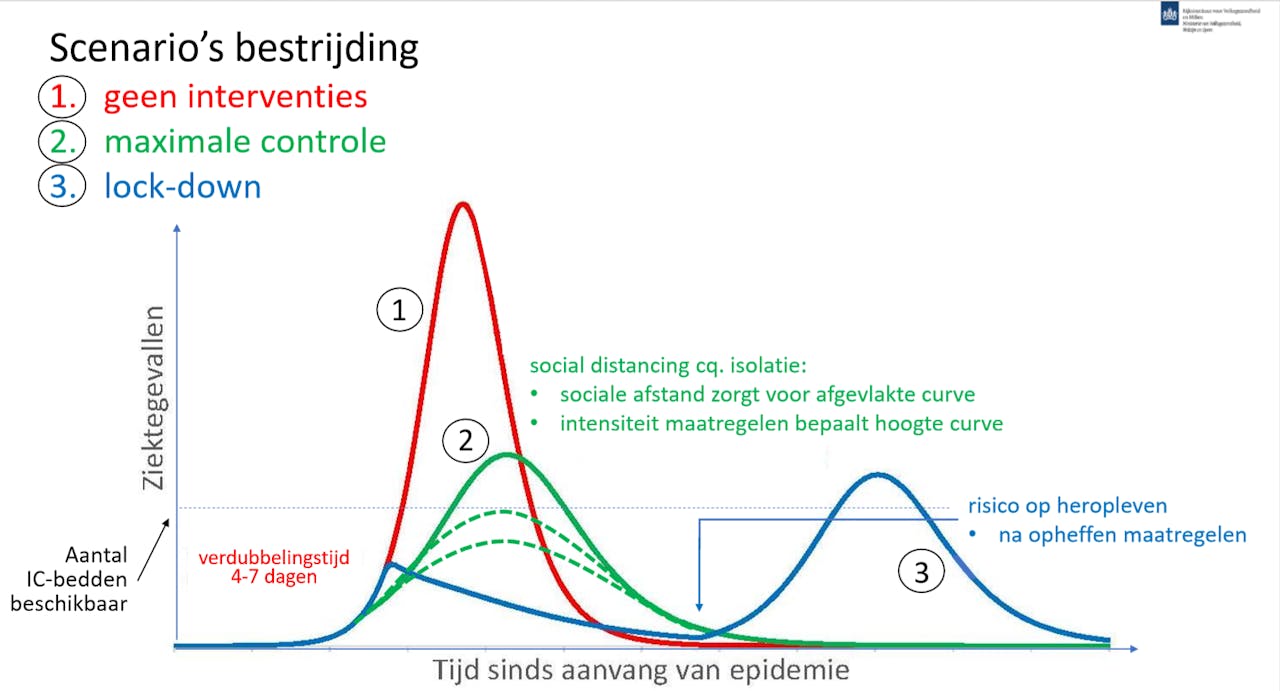
Dit is de reden dat het probleem met het aantal ziekenhuisbedden binnen een paar dagen van ‘onder controle’ naar ‘volstrekt ontoereikend’ kan gaan – én de reden dat we zo veel mogelijk binnen moeten blijven en 1,5 meter afstand van elkaar moeten houden. Het feit dat mensen elkaar na gemiddeld 5 dagen kunnen besmetten, betekent dat je in je eentje binnen 50 dagen verantwoordelijk kan zijn voor meer dan duizend virusdragers.
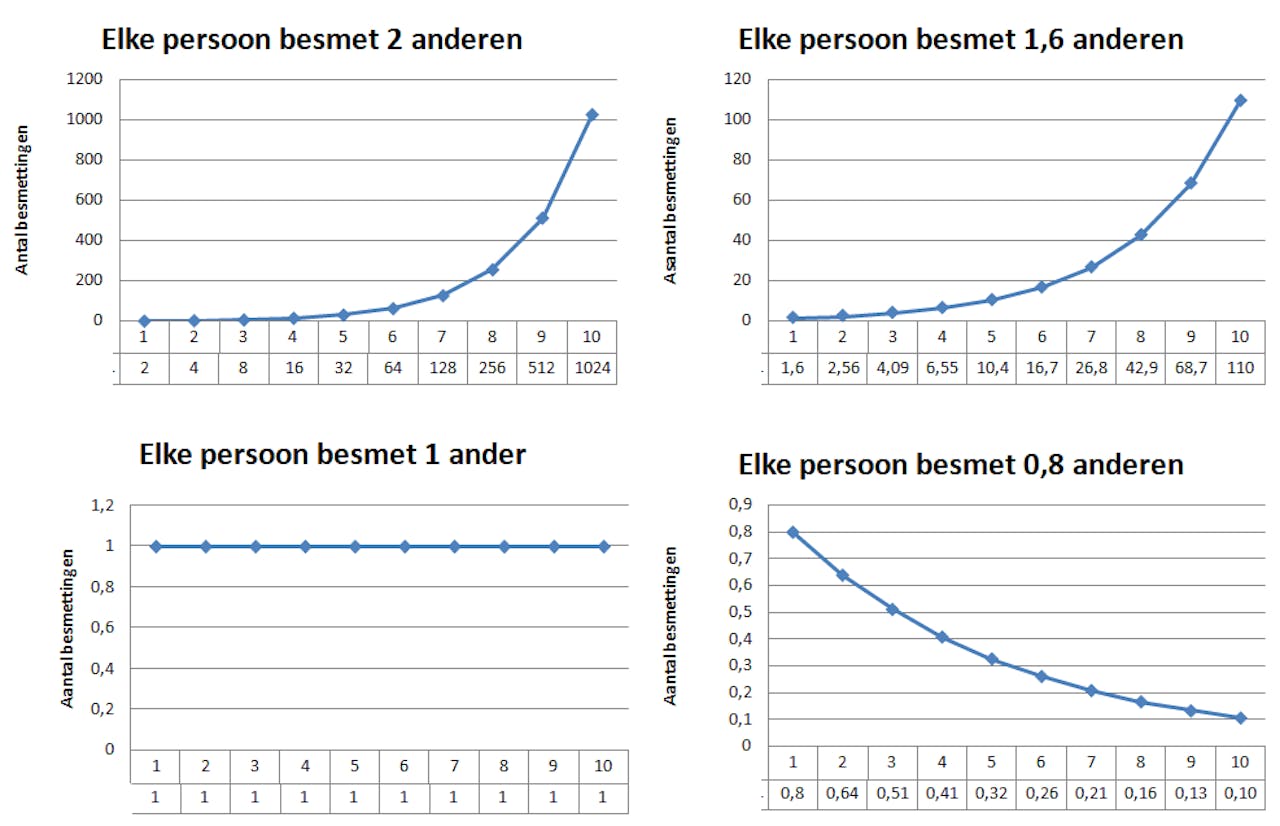
Het aantal nieuwe besmettingen na 10 overdrachten, bij verschillende waarden voor de besmettingsgraad (Let op: y-as per plaatje verschillend). Een besmettingsgraad van 0,8 betekent dat elke tien mensen samen gemiddeld acht anderen besmetten.
Marlies ter Voorde, voor NEMO KennislinkAls we het gemiddelde aantal virusoverdrachten per persoon omlaag kunnen krijgen, van twee naar 1,6 bijvoorbeeld, scheelt dat na tien overdrachten al 914 nieuwe besmettingen, en zit je na vierentwintig overdrachten ‘pas’ op 80.000. Als we gemiddeld allemaal nog maar één persoon kunnen besmetten blijft het aantal nieuwe gevallen zelfs constant – en als we onder de één kunnen duiken, zullen het er langzaam maar zeker minder worden.
Tot zover de bierviltjesberekeningen, die de afgelopen weken haast nog sneller viraal zijn gegaan dan de corona zelf.
Biologisch groeimodel
Maar er zijn meer redenen waarom het aantal mensen dat een virus oploopt uiteindelijk kan stabiliseren. Als een virus wel genoeg mensen kan vinden om op over te stappen maar deze immuun zijn geworden bijvoorbeeld – doordat ze de ziekte al gehad hebben, of omdat er een vaccin is (hoewel dat laatste waarschijnlijk nog minstens een jaar gaat duren). Het overgesprongen virusdeeltje zal dan door deze mensen onschadelijk gemaakt worden, en het virus zal uiteindelijk dus steeds minder overstaproutes tot zijn beschikking hebben. Dit doet de gemiddelde besmettingsgraad dalen, waarmee het nog niet geïnfecteerde deel van de bevolking steeds beter beschermd wordt door de immuun geworden mensen er om heen: dit is de groepsimmuniteit, waar premier Rutte het in zijn toespraak op 15 maart over had.
Op verschillende plekken in het land zijn statistici gaan rekenen aan dit scenario, gebruik makend van het ‘biologische groeimodel’ – een wiskundige formule die zowel de snelle groei aan het begin als de afvlakking na verloop van tijd beschrijft. Deze functie, die bijvoorbeeld ook wordt gebruikt om de groei van konijnenpopulaties (die afvlakt door voedselgebrek) te beschrijven, werd halverwege de negentiende eeuw ontwikkeld door de Belgische wiskundige Pierre François Verhulst. De curve zier eruit als een S, waarvan de exacte vorm bepaald wordt door het uiteindelijke (totale) aantal besmettingen en de snelheid van de groei. Onder anderen statistici van de Technische Universiteit Eindhoven zijn hiermee aan het rekenen geslagen, waarbij ze de situatie van de komende drie dagen inschatten (en dagelijks bijstellen) uit de vorm die de curve tot nu toe heeft aangenomen.
De modellen van het RIVM
De maatregelen die we van de overheid opgelegd krijgen, zijn niet gebaseerd op adviezen van de bierviltjesrekenaars of de statistici, maar van de epidemiologen en virologen van het RIVM. Ook hun modellen zijn gebaseerd op de exponentiële groei van het virus en een afvlakking als er immuniteit optreedt of mensen minimaal contact hebben, maar dan aangevuld met gedetailleerder kennis van de opbouw en het gedrag van de Nederlandse bevolking. De ziekte verloopt immers anders bij jongeren dan bij ouderen, kinderen lijken vooralsnog minder besmettelijk te zijn, en de sociale interactie tussen mensen verschilt per leeftijd en regio.
De wetenschappers van het RIVM voeden hun modellen daarom ook met de leeftijdsopbouw van de Nederlandse bevolking, met daaraan gekoppeld (per geboortejaar en geslacht) het percentage personen dat extra risico loopt, het gemiddelde aantal contacten per dag, en de setting van die contacten (bijvoorbeeld op school, thuis of in de bioscoop).
Dan nog blijft het een kwestie van ijken, bijstellen en interpreteren. Het modelleren van deze crisis is als rijden in de mist. Het virus is nieuw, wat we er over weten is voornamelijk gebaseerd op de eerste uitbraak in China, maar de kennis blijkt voortdurend te moeten worden bijgesteld. Zo ging het RIVM er in eerste instantie van uit dat je pas anderen kan besmetten als je zelf ziekteverschijnselen hebt, maar blijkt een deel van de besmettingen al in de fase daarvoor plaats te hebben gevonden. Ook de vraag hoe lang een eventuele immuniteit aanhoudt staat nog open.
Daarnaast kunnen bijzondere omstandigheden de waarden van de parameters beïnvloeden: Zo was het besmettingsgetal tijdens carnaval in Brabant lokaal en tijdelijk fors boven het gemiddelde, en zijn de sterftecijfers per land verschillend door de manier van registreren, de bevolkingsopbouw, en de kwaliteit van de gezondheidszorg.
Het RIVM neemt de onzekerheden mee in de modellen, die uiteindelijk dus een hele range aan curves opleveren, en niet één strakgetrokken lijn. Op welke van deze curves we terechtkomen weten we bovendien pas geruime tijd nadat een maatregel is ingezet, omdat we te maken hebben met meerdere vertragingsfactoren: tussen een besmetting en het krijgen van ziekteverschijnselen zit een dag of vijf, daarna duurt het gemiddeld een week tot een eventuele opname in het ziekenhuis. De tijd tussen het nemen van maatregelen en het sterftecijfer kan uiteindelijk oplopen tot een maand.
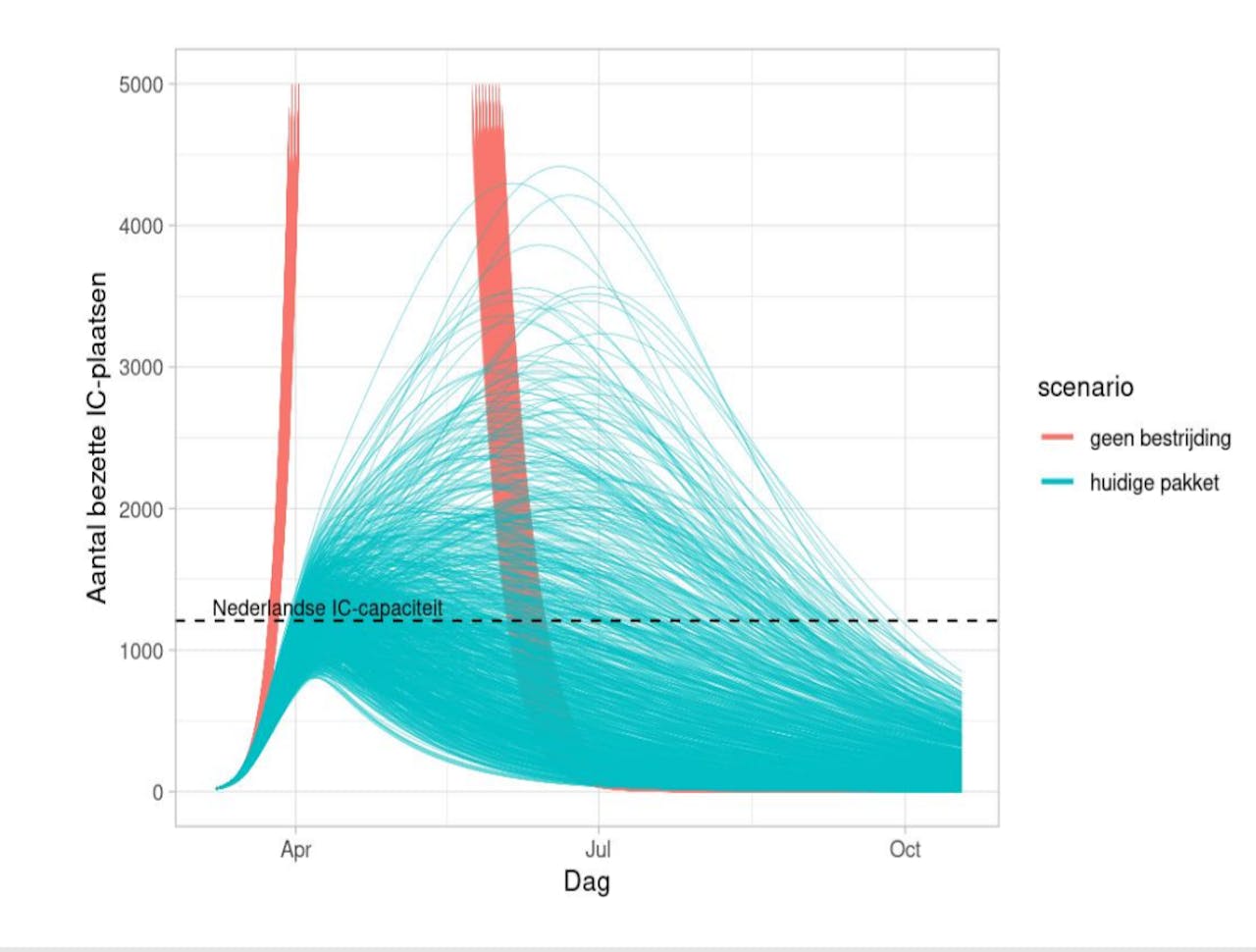
Onzekerheden in modelparameters zoals besmettingsgraad en verdubbelingstijd leiden tot onzekerheden in de resultaten (in dit geval benodigde IC-bedden). Deze figuur is de doorrekening van de maatregelen die tot 23 maart golden (en die daarna dus verscherpt zijn).
RIVM (Rijksinstituut voor Volksgezondheid en Milieu)“Het is afwachten”, heeft Jaap van Dissel, directeur van het Centrum Infectiebestrijdig van het RIVM, al meermalen gezegd. “We moeten met vijftig procent van de kennis honderd procent van de besluiten nemen”, stelde premier Mark Rutte vorige week in zijn toespraak tot het volk.
Veel is dus onzeker. Maar dat je voorlopig contacten moet mijden en afstand moet houden staat vast.