Aan de slag met vraag 7 van de Wetenschapsquiz

Eerst maar het flauwe antwoord afhandelen: als je de tegels ook mag omkeren – dus ze oppakken en met de bovenkant onderop weer neerleggen, wiskundig gezien komt dit neer op spiegelen – zijn alledrie de antwoorden mogelijk, en is de vraag onzinnig. Je kunt dan namelijk met alleen strikjes een oneindig groot vlak betegelen, of met alleen bootjes, of met een bijna willekeurige mix van die twee. Het staat er weliswaar niet bij dat omkeren niet mag, maar laten we daar maar vanuit gaan. Deze triviale oplossingen maken ondertussen wel duidelijk, dat het probleem zit in de kleine in- en uithammetjes, die er voor zorgen dat je twee tegels niet met elke zijde tegen elkaar aan kan leggen.

Los daarvan: hoe tel je überhaupt het aantal tegels van de ene en de andere soort op een oneindig vlak? Dan heb je van beide soorten oneindig veel tegels nodig, en de verhouding tussen beide, ‘oneindig gedeeld door oneindig’, heeft geen uitkomst.

Periodieke betegelingen

Voor periodieke betegelingen, zoals in het plaatje hiernaast, is het simpel. Een betegeling is periodiek als hetzelfde patroon eindeloos herhaald wordt. De kleinste repeterende eenheid van bovenstaand patroon is een strikje met zijn spiegelbeeld (het gearceerde stuk). Die vormt een basistegel waarmee je een oneindig vlak kunt bedekken zonder dat er gaten overblijven. Voor het hele vlak heb je dus strikjes en gespiegelde strikjes nodig in de verhouding 1:1.

Wat leert ons dit over de betegeling uit de Wetenschapsquiz, waar we de tegels niet mogen spiegelen? Kunnen we met een beperkt aantal strikjes en bootjes een basistegel maken die het hele vlak bedekt?

Als je niet gehinderd door inzicht maar wat aan het tegelen slaat, ontstaat – doordat de in- en uithammetjes in elkaar moeten passen – een soort geschubd patroon van rondjes die elk uit drie bootjes en een strikje bestaan, maar die rondjes kunnen in hun eentje geen vlak betegelen, de gaten daartussen moet je opvullen met extra strikjes. Maar dan nog lukt het niet zomaar om het hele vlak vol te leggen. In afbeelding 3, bijvoorbeeld, past het losse rondje rechtsboven niet meer aan het geheel, omdat de in- en uithammen niet overeen komen.

Valt in dit patroon al een basistegel te herkennen? Misschien twee rondjes met een strikje ertussen? Drie of vier rondjes met een of meer strikjes ertussen? Het lijkt er toch sterk op, dat het patroon telkens verspringt. Door alleen maar te kijken, weet je natuurlijk nooit zeker of er niet een veel grotere basistegel bestaat, zeg van 171 strikjes en 297 bootjes, waarvan dit patroon alleen maar een fragment is. Of misschien bestaat er wel een simpele basistegel, maar komt die alleen tevoorschijn als je van het begin af aan slimmer tegelt. Probeer dit vooral zelf, maar het vermoeden rijst toch dat hier iets anders aan de hand is, namelijk dat dit een Penrose-betegeling is.

Niet-periodieke betegelingen

Roger Penrose is een Britse wiskundige die rond 1970 ontdekte dat je met slechts twee slim ontworpen tegels kunt afdwingen, dat een betegeling van het oneindige vlak niet-periodiek is. Dit klinkt vrij onschuldig, maar voordien vermoedde men niet eens dat zoiets mogelijk is (voorlopers van Penrose had kort daarvoor ook geëxperimenteerd met niet-periodieke betegelingen, maar die hadden veel meer verschillende tegels nodig).

Niet-periodiek betekent namelijk, dat het tegelpatroon zich nergens identiek herhaalt. Er is geen basistegel, hoe groot ook, waarmee je het complete oneindige patroon kunt leggen. Als de strikjes-bootjes betegeling niet-periodiek is, komt elke combinatie van strikjes en tegels ergens op het oneindige vlak voor – oneindig vaak zelfs – maar daartussen zitten altijd ook gaten die je met weer andere combinaties van strikjes en tegels op moet vullen.

Dat betekent ook, dat de verhouding tussen het aantal strikjes en bootjes afhangt van welk gebied je bekijkt, er is geen exact getal voor te geven. Het feit, dat antwoorden b en c van de vraag in de Wetenschapsquiz alleen een boven- en een ondergrens geven voor die verhouding, kun je zien als een extra aanwijzing dat dit inderdaad een Penrose-betegeling is.

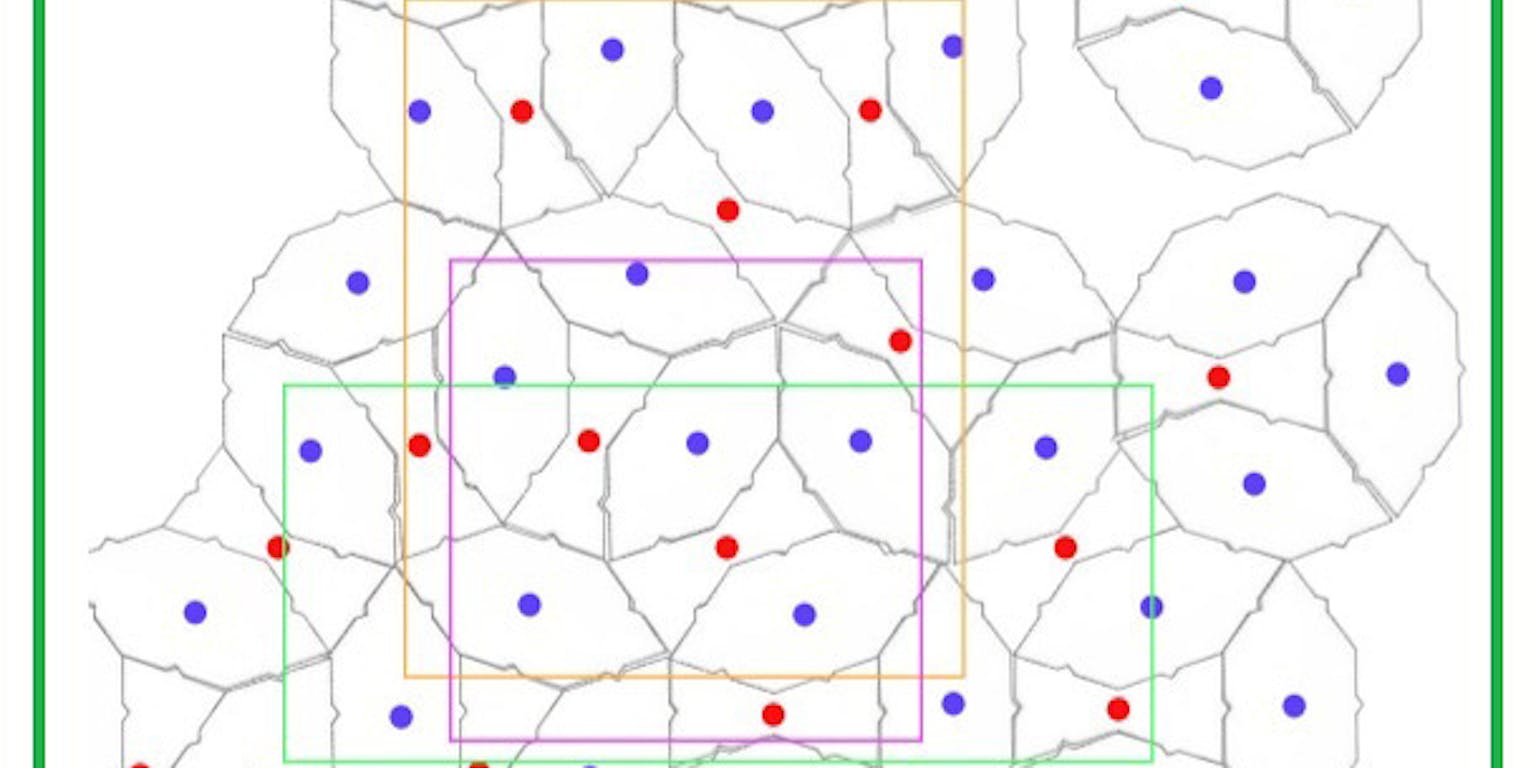
Als de verhouding niet exact te bepalen is, hoe groot is die dan ongeveer? Als je aanneemt dat het tegelpatroon in afbeelding 3 representatief is voor de oneindige betegeling, kun je er een steekproef op loslaten. In afbeelding 5 zijn drie willekeurige rechthoeken getrokken, en de middelpunten van de strikjes zijn aangegeven met rood, die van de bootjes met blauw. Je kunt nu simpelweg turven wat de verhouding strikjes/bootjes is in elk van de drie rechthoeken. De score die daar uit komt wijst duidelijk op één van de drie antwoorden a,b of c.