Vrijwel iedereen heeft tegenwoordig een Facebookaccount. Hoe ziet jouw Facebooknetwerk er eigenlijk uit? En wat hebben deze netwerken te maken met wiskunde?
Dit plaatje geeft mijn Facebookprofiel als een netwerk weer: een aantal punten met lijnen ertussen. De punten zijn al mijn Facebookvrienden. Twee van mijn Facebookvrienden zijn verbonden door een lijn als ze ook bevriend zijn met elkaar op Facebook.
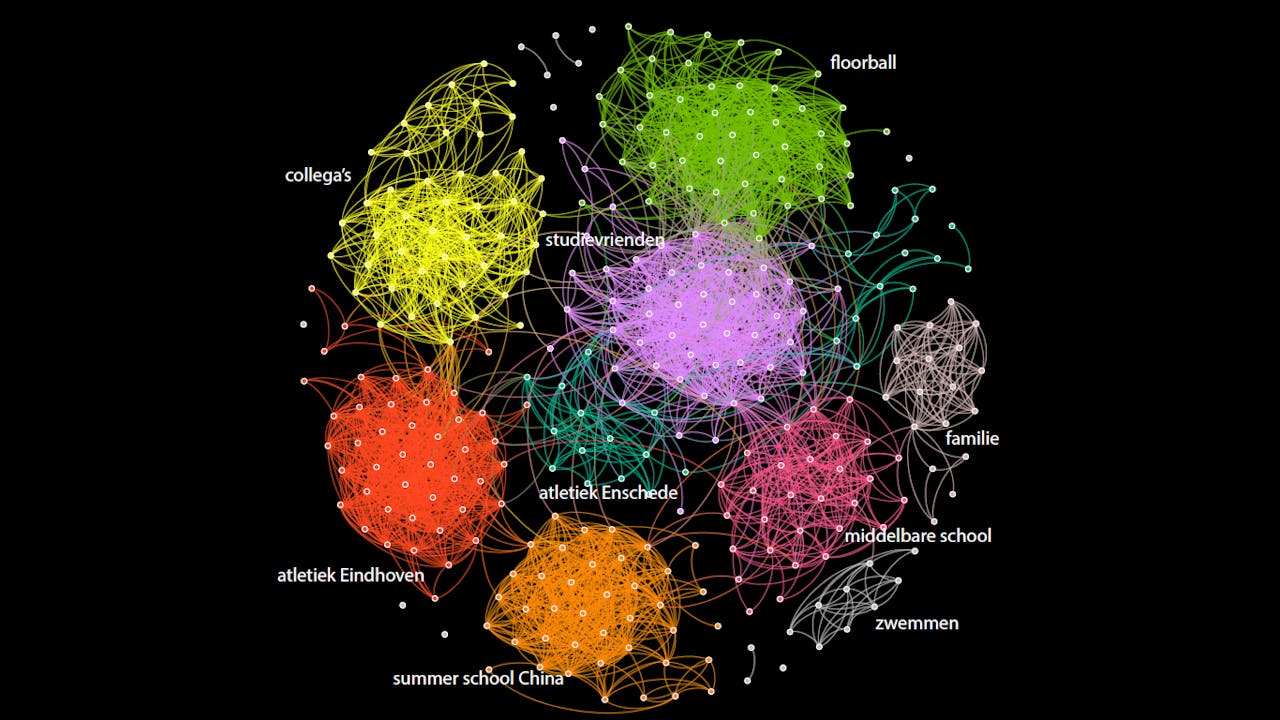
Het Facebooknetwerk van Clara
Clara Stegehuis voor NEMO KennislinkOnverwachte verbindingen
Het is best leuk om zo terug te zien waar ik allemaal mensen heb leren kennen. Zo zie je dat ik allerlei verschillende sporten geprobeerd heb, en een aantal keer verhuisd ben. Mensen die ik op een bepaalde plaats heb ontmoet, kennen elkaar vaak goed. Hierdoor ontstaan groepsstructuren, groepen van punten die met heel veel lijnen verbonden zijn.
Toch zijn er ook best veel verbindingen tussen de verschillende groepen die ik zelf niet had verwacht. Zo kent een van mijn neefjes blijkbaar iemand met wie ik in Enschede op atletiek heb gezeten. En kent iemand die ik een keer in China heb ontmoet iemand die bij mij op de middelbare school in de klas heeft gezeten.
Wiskunde in enorme netwerken
Mijn onderzoek gaat over netwerken, dus punten die door lijnen zijn verbonden. Dit kunnen mensen zijn die elkaar kennen op sociale media, zoals in het bovenstaande plaatje. Maar in de komende blogs laat ik zien dat er ook heel veel andere toepassingen zijn van netwerken. Vaak zijn die netwerken ongelofelijk groot. Het plaatje van mijn vriendennetwerk is nog wel te overzien, dit zijn namelijk “maar” 317 punten. Maar als je alle Facebookgebruikers over de hele wereld als een netwerk bekijkt, zoals hieronder, dan heeft dit netwerk ongeveer twee miljard punten!
Als je alle Facebookgebruikers over de hele wereld als een netwerk bekijkt, dan heeft dit netwerk ongeveer twee miljard punten!
John Haydon via Flickr CC BY-NC-SA 2.0Doordat die netwerken zo groot zijn, is het moeilijk om er nog iets zinnigs in terug te zien. Daarom proberen we deze netwerken te beschrijven met wiskundige vergelijkingen. Het gekke is namelijk dat het voor wiskundigen juist veel makkelijker is om aan hele grote netwerken te rekenen dan aan bijvoorbeeld mijn relatief kleine vriendennetwerk. Met deze wiskundige berekeningen hopen we meer te weten te komen over grote netwerken. Wat vertelt wiskunde ons bijvoorbeeld over hoe een Facebookpost viral gaat? En hoe vinden we de groepsstructuren in hele grote netwerken? Dit soort vragen probeer ik in mijn onderzoek te beantwoorden.
Je eigen netwerk bekijken
Wil je kijken of jouw eigen Facebooknetwerk net zulke groepsstructuren heeft? Of er verbindingen zijn die je misschien niet had verwacht? In Google Chrome kun je deze plugin downloaden die meteen een plaatje van je Facebooknetwerk maakt.