Ik kan beter over problemen nadenken wanneer ik het plaatje voor me zie. Ik gebruik liever een visuele representatie van informatie dan dat ik een lap tekst door lees. Zo kijk ik liever naar een routekaart, dan een lijst met instructies die mij vertellen hoe ik van A naar B kom.
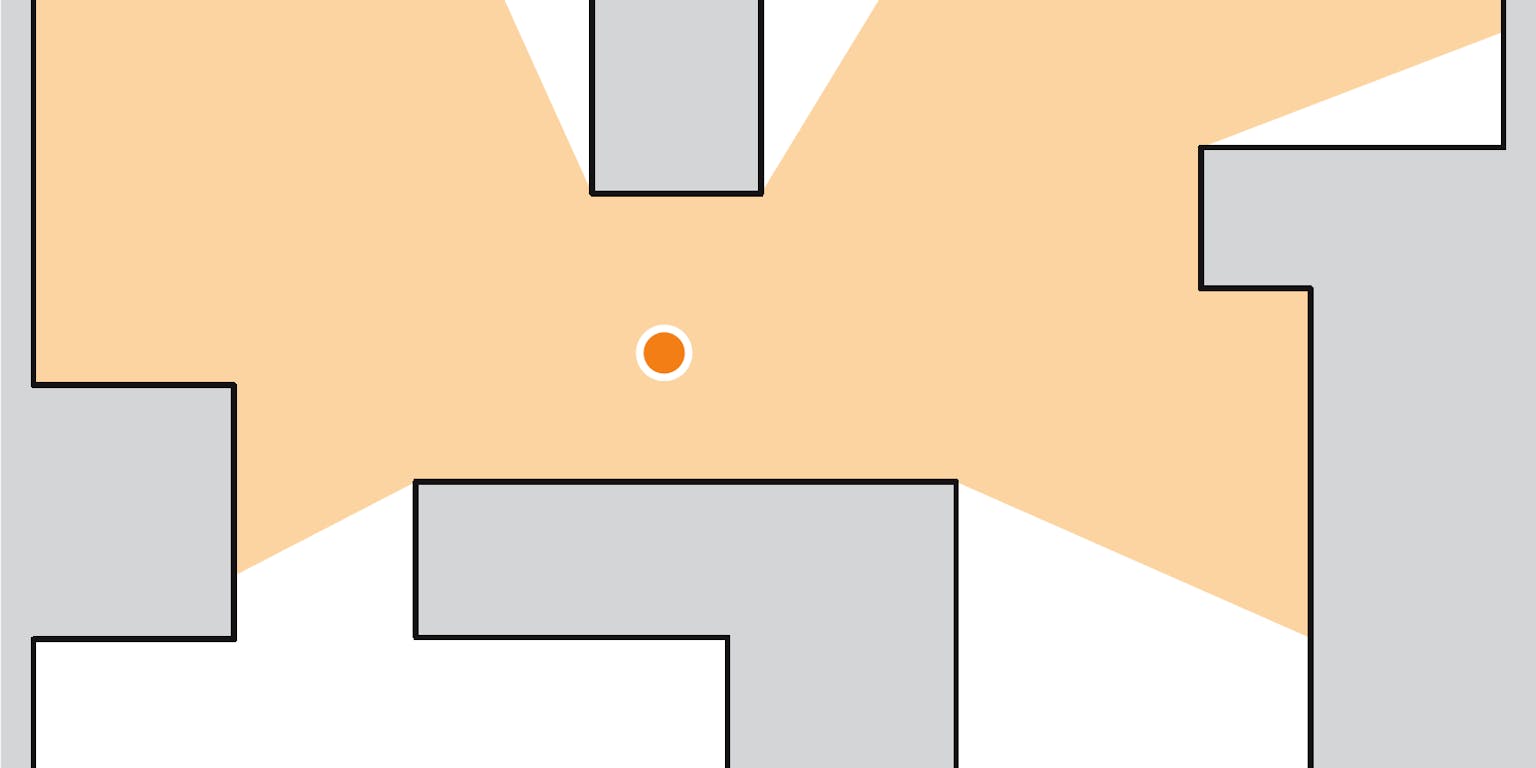
Hoeveel camera’s zijn nodig voor deze plattegrond? De camera’s kunnen 360 graden om zich heen kijken, maar niet door muren. Als voorbeeld staat er vast een camera (niet op de juiste plek). Voor antwoord: zie onderaan pagina.
Wouter Meulemans voor NEMO KennislinkMuseumprobleem
De algoritmische problemen die ik onderzoek heb dan ook vaak een geometrisch karakter. De vraag wordt geformuleerd door gebruik te maken van punten, lijnen en vlakken. Een typisch voorbeeld is het museumprobleem (art gallery problem). Je hebt een plattegrond van een galerij en de uitdaging is om camera’s op te hangen zodat het hele museum in de gaten gehouden kan worden. Je kunt op elke vierkante centimeter een camera plaatsen, maar dit is natuurlijk niet een goede oplossing. Je plaatst het liefst zo min mogelijk camera’s zodat toch alles bewaakt wordt.
Hoeveel camera’s heb je minimaal nodig voor bovenstaande plattegrond? Ze kunnen 360 graden om zich heen kijken, maar niet door muren :). De oplossing staat onderaan deze pagina.
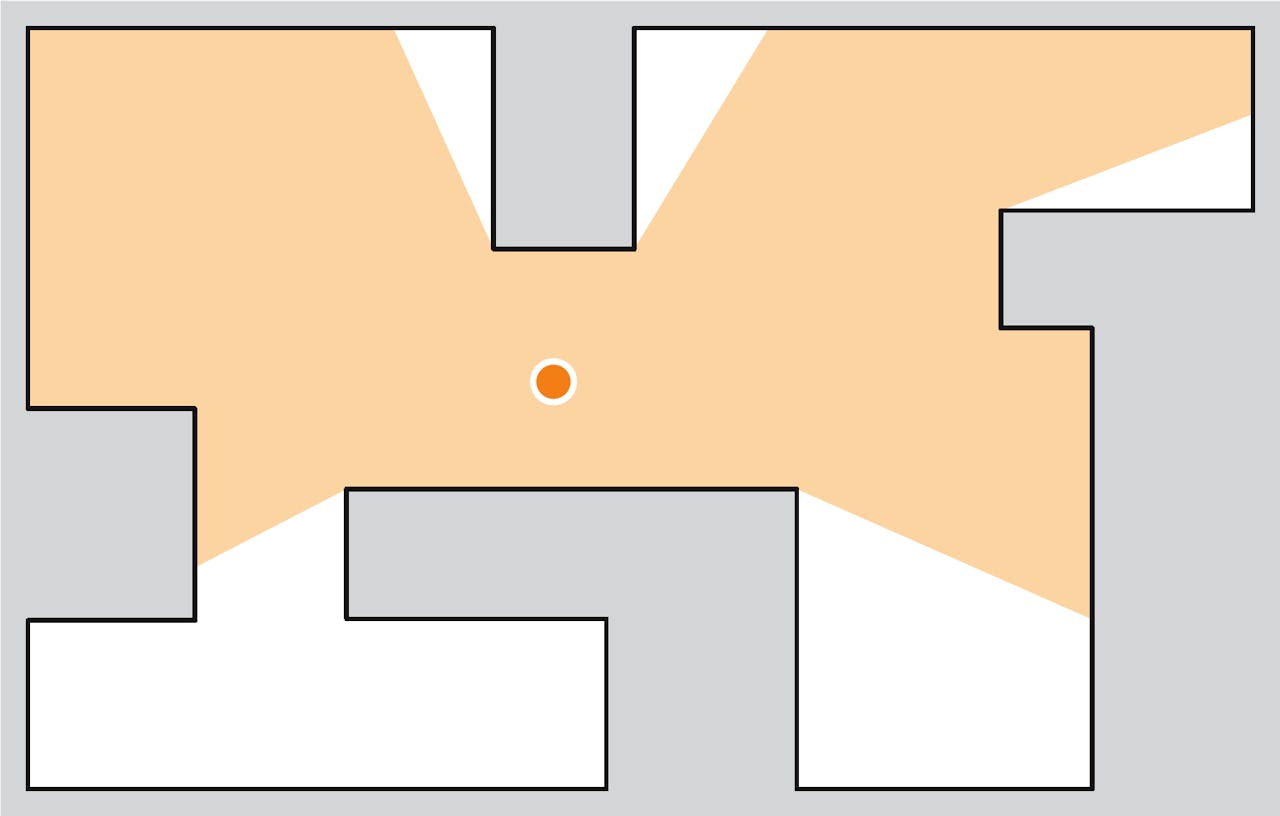
En hoeveel heb je er nodig voor onderstaande plattegrond? Houd voor het antwoord mijn blog in de gaten!

Deze plattegrond is al lastiger. Hoeveel camera’s heb je hiervoor nodig?
Wouter Meulemans voor NEMO Kennislink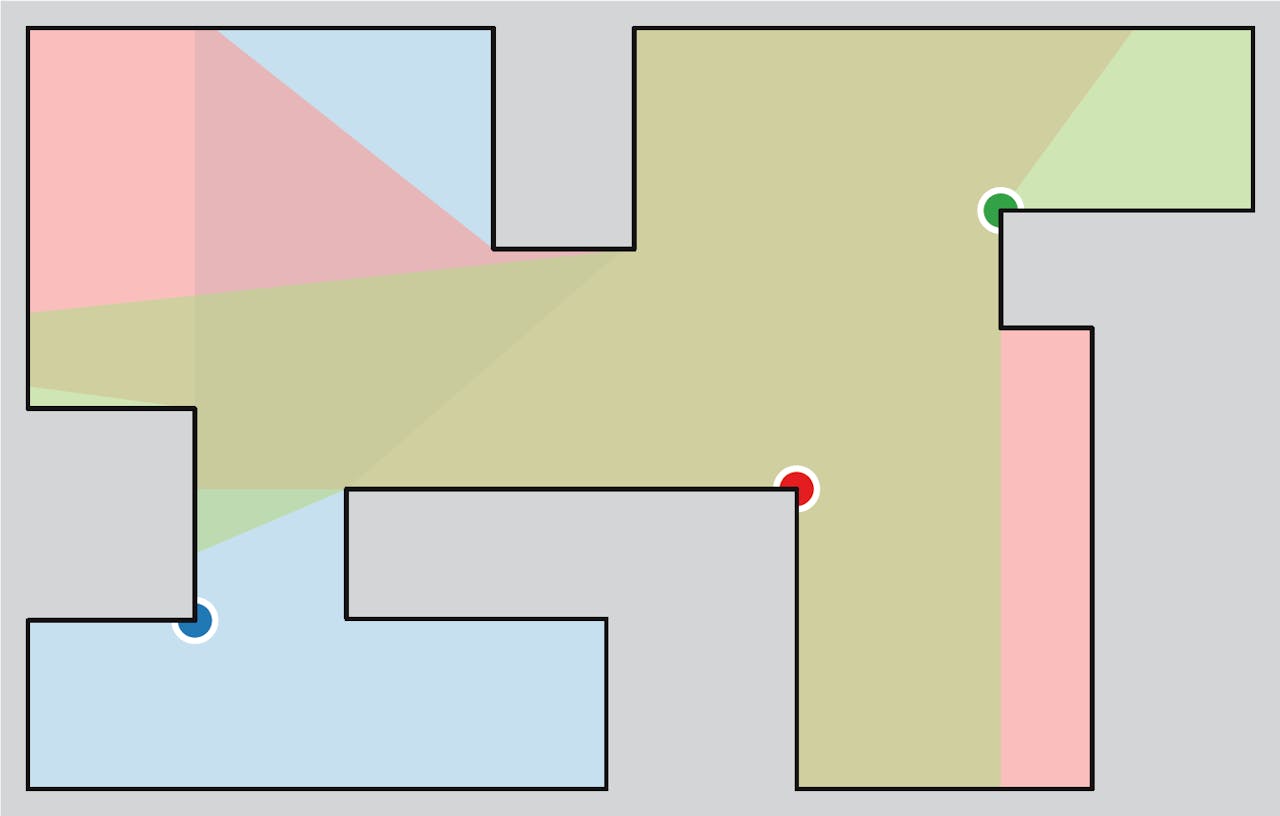
Oplossing eerste puzzel: Je hebt slechts 3 camera’s nodig!
Wouter Meulemans voor NEMO Kennislink